Формула варијансе становништва | Корак по корак | Примери
Формула за израчунавање варијансе становништва
Формула варијансе становништва мери се просечним удаљеностима података о становништву и израчунава се утврђивањем средње вредности формуле популације, а варијанса се израчунава збиром квадрата променљивих минус средња вредност која је подељена бројем посматрања у популацији.
Варијација становништва је мера ширења података о становништву. Стога се варијанса популације може дефинисати као просек удаљености од сваке тачке података у одређеној популацији до средње вредности, на квадрат и показује како су тачке података распоређене у популацији. Варијација становништва је важна мера дисперзије која се користи у статистици. Статистичари израчунавају варијансу да би утврдили у каквом су односу поједини бројеви у скупу података.
При израчунавању варијансе популације, дисперзија се израчунава у односу на средњу вредност популације. Стога морамо да сазнамо средњу вредност популације да бисмо израчунали варијансу популације. Једно од најпопуларнијих обавештења о варијанси становништва је σ2. Ово се изговара као сигма на квадрат.
Одступање становништва може се израчунати помоћу следеће формуле:


где
- σ2 је варијанса популације,
- Икс1, Икс2, Икс3,…..Иксн су запажања
- Н је број посматрања,
- µ је средина скупа података
Корак по корак израчунавања варијансе становништва
Формула за варијансу популације може се израчунати помоћу следећих пет једноставних корака:
- Корак 1: Израчунати средњу вредност (µ) датих података. Да бисте израчунали средњу вредност, додајте сва запажања, а затим поделите то са бројем посматрања (Н).
- Корак 2: Направи сто. Имајте на уму да израда табеле није обавезна, али представљање у табеларном формату олакшало би прорачуне. У прву колону напишите свако запажање (к1, Икс2, Икс3,…..Иксн).
- Корак 3: У другу колону напишите одступање сваког посматрања од средње вредности (ки - µ).
- Корак 4: У трећу колону упишите квадрат сваког посматрања из средње вредности (ки - µ) 2. Другим речима, квадрат сваки од бројева добијених у колони 2.
- Корак 5: После тога морамо додати бројеве добијене у трећој колони. Наћи збир квадратних одступања и тако добијени збир поделити са бројем посматрања (Н). Ово ће нам помоћи да то добијемо
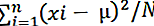 што је варијанса популације.
што је варијанса популације.
Примери
Овде можете преузети овај образац Екцел варијабле популације, образац Екцел Екцел шаблонаПример # 1
Израчунајте варијансу популације из следећих 5 посматрања: 50, 55, 45, 60, 40.
Решење:
За израчунавање варијансе популације користите следеће податке.

Укупно има 5 запажања. Дакле, Н = 5.
µ = (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
Дакле, прорачун варијансе популације σ2 може се извршити на следећи начин -


σ2 = 250/5
Варијанса становништва σ2 биће-

Одступање становништва (σ2) = 50
Одступање становништва износи 50.
Пример # 2
КСИЗ доо је мала фирма која се састоји од само 6 запослених. Генерални директор сматра да не би требало да дође до велике дисперзије у платама ових запослених. У ту сврху жели да израчунате одступање ових зарада. Плате ових запослених су као испод. Израчунајте варијансу зарада међу извршним директорима у популацији.
Решење:
За израчунавање варијансе популације користите следеће податке.

Постоји укупно 6 запажања. Дакле, Н = 6.
=(30+27+20+40+32+31)/6 =180/6 =$ 30
Дакле, прорачун варијансе популације σ2 може се извршити на следећи начин -


σ2 = 214/6
Варијанса становништва σ2 биће-

Одступање становништва (σ2) = 35,67
Одступање зарада у становништву је 35,67.
Пример # 3
Свеет Јуице Лтд производи различите укусе сокова. Одељење за менаџмент купује 7 великих контејнера за складиштење овог сока у фабрици. Одељење за контролу квалитета одлучило је да ће одбити контејнере ако је одступање контејнера веће од 10. С обзиром на тежину 7 контејнера у кг: 105, 100, 102, 95, 100, 98 и 107. Молимо вас да саветујете квалитет Контролно одељење да ли треба да одбаци контејнере.
Решење:
За израчунавање варијансе популације користите следеће податке.

Укупно има 7 запажања. Дакле, Н = 7
=(105+100+102+95+100+98+107)/7 =707/7 =10
Дакле, израчунавање варијансе популације σ2 може се извршити на следећи начин -


σ2 = 100/7
Варијанса становништва σ2 биће-

Одступање становништва (σ2) = 14,29
Будући да је одступање (14,29) веће од ограничења од 10 које је одредио Одељење за контролу квалитета, контејнере треба одбити.
Пример # 4
Управни тим болнице под именом Сагар Хеалтхцаре забележио је да је у првој недељи марта 2019. рођено 8 беба. Лекар је желео да процени здравље беба као и варијансу висине. Висине ове бебе су следеће: 48 цм, 47 цм, 50 цм, 53 цм, 50 цм, 52 цм, 51 цм, 60 цм. Израчунајте варијансу висине ових 8 беба.
Решење:
За израчунавање варијансе популације користите следеће податке.

Дакле, прорачун варијансе популације σ2 може се извршити на следећи начин -

У програму Екцел постоји уграђена формула за варијансу популације која се може користити за израчунавање варијансе популације групе бројева. Изаберите празну ћелију и откуцајте ову формулу = ВАР.П (Б2: Б9). Овде је Б2: Б9 опсег ћелија из којег желите да израчунате варијансу популације.
Варијанса становништва σ2 биће-

Варијација становништва (σ2) = 13.98
Релевантност и употреба
Одступање становништва се користи као мера дисперзије. Размотримо два скупа популације са истим средњим вредностима и бројем посматрања. Скуп података 1 састоји се од 5 бројева - 55, 50, 45, 50 и 50. Скуп података 2 састоји се од 10, 50, 85, 90 и 15. Оба скупа података имају исту средњу вредност, која је 50. Али, у скупу података 1 вредности су близу једна другој док скуп података 2 има расејане вредности. Варијанса даје научну меру ове блискости / дисперзије. Скуп података 1 има варијансу од само 10, док скуп података 2 има огромну варијансу од 1130. Дакле, велика варијанса указује на то да су бројеви далеко од средње вредности и једни од других. Мала варијанса указује на то да су бројеви близу један другом.
Варијанса се користи у пољу управљања портфељем током извршавања алокације имовине. Инвеститори израчунавају варијансу приноса на имовину како би одредили оптималне портфеље оптимизацијом два главна параметра - приноса и волатилности. Волатилност мерена варијансом је мера ризика одређеног финансијског осигурања.

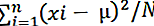 што је варијанса популације.
што је варијанса популације.