photosdematures.com

НПВ вс КСНПВ

Нето садашња вредност (НПВ) дефинисана је као разлика између постојеће вредности нето новчаних долазака и постојеће вредности укупних новчаних издатака. Иако је НПВ најкориснији у случају периодичних новчаних токова, КСНПВ, с друге стране, одређује нето садашњу вредност за низ новчаних плаћања која у суштини не морају бити периодична.

У овом чланку ћемо детаљно размотрити НПВ вс КСНПВ -

Такође, погледајте НПВ вс ИРР

Шта је НПВ?

Нето садашња вредност (НПВ) дефинисана је као разлика између постојеће вредности нето новчаних долазака и постојеће вредности укупних новчаних издатака. НПВ се обично користи приликом припреме процена капиталног буџета за тачно одређивање одрживости било ког новог пројекта или потенцијалне могућности улагања.

Формула за одређивање НПВ (када су готовински доласци парни):

НПВ_{т = 1 до Т.} = ∑ Кст / (1 + Р) т - Ксо

Где,

• Икс_т = укупан прилив готовине за период т
• Икс_о = нето почетни инвестициони издаци
• Р = дисконтна стопа, коначно
• т = укупан број временских периода

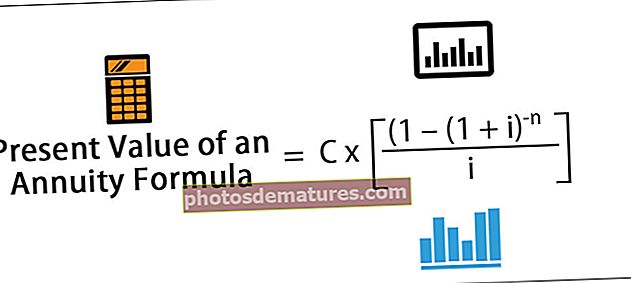
Формула за одређивање НПВ (када су приходи готовине неравномерни):

НПВ = [Ц._и1/ (1 + р) 1 + Ц._и2/ (1 + р) 2 + Ц._и3/ (1 + р) 3 +…] - Кс_о

Где,

• Р је наведена стопа поврата по периоду;
• Ц._и1 је консолидовани готовински долазак током првог периода;
• Ц._и2 је консолидовани готовински долазак током другог периода;
• Ц._и3 је консолидовани долазак готовине током трећег периода, итд ...

Избор пројеката коришћењем НПВ

За појединачне пројекте, узмите пројекат једноставно када се НПВ израчуна као позитиван, одбаците га ако је НПВ израчунат као негативан и останите равнодушни према разматрању или одбацивању ако је НПВ пројекта достигао нулу.

За потпуно различите пројекте или конкурентске пројекте, узмите у обзир да пројекат има већу НПВ.

Нето садашња вредност са позитивним предзнаком означава да процењена зарада остварена било којом инвестицијском приликом или пројектом (у постојећим апоенима долара) премашује предвиђене трошкове (такође у постојећим вредностима долара). Обично ће свака инвестиција која има позитивне НПВ резултате бити уносна, док би она која има негативне НПВ резултате довела до укупног губитка. Ова идеја посебно дефинише правило нето садашње вредности, указујући да се морају узети у обзир само она улагања која имају позитивне НПВ резултате.

Поред тога, претпоставимо да је могућност улагања повезана са спајањем или припајањем, чак се може применити и Дисконтовани новчани ток.

Поред НПВ формуле, нето садашња вредност може се чак израчунати коришћењем прорачунских табела, табела као што је Мицрософт Екцел, као и НПВ калкулатора.

Коришћење НПВ у програму Екцел

Коришћење НПВ у екцел листу је врло једноставно.

= НПВ (стопа, вредност1, вредност2, вредност3 ..)

• Стопа у формули је дисконтна стопа која се користи у једном периоду
• Вредност 1, Вредност 2, Вредност 3 итд. Су новчани приливи или одливи на крају периода 1, 2, 3, респективно.

НПВ Пример # 1 - са наведеним предефинисаним приливом готовине

Претпоставимо да компанија жели да анализира процењену одрживост кључног пројекта који захтева рани одлив од 20.000 долара. Током периода од три године чини се да пројекат доноси приходе од 4000, 14.000 и 22.000 долара, респективно. Предвиђена дисконтна стопа очекује се на 5,5%. На први поглед изгледа да су поврати од улагања готово двоструко већи од почетних улагања. Али, износ зарађен током три године остаје исте вредности као данас зарађени нето износ, па рачуновођа компаније одређује НПВ на јединствен начин за идентификовање укупне профитабилности, док, израчунавајући смањену временску вредност процењених прихода:

Пример НПВ 1 - Решење помоћу ручног израчунавања

Да бисте израчунали нето садашњу вредност, треба имати на уму следеће тачке:

• Збир примљене садашње вредности
• Одбитак садашње вредности која се плаћа

НПВ = {4.000 УСД / (1 + .055) ^ 1} + {14.000 УСД / (1 + .055) ^ 2} + {22.000 УСД / (1 + .055) ^ 3} - 20.000 УСД

= $3,791.5 + $12,578.6 + $18,739.4 – $20,000

= $15,105.3

НПВ Пример # 1 - Решење користећи Екцел

Решавање НПВ проблема у програму Екцел је врло једноставно. Прво, треба да ставимо променљиве у стандардни формат као што је дато у наставку са Новчаним токовима у један ред.

У овом примеру добијамо дисконтну стопу од 5% годишње. Када користимо НПВ Формулу, почињемо са 4000 УСД (приливи готовине на крају 1. године) и бирамо опсег до 22.000 УСД (

Када користимо НПВ Формулу, почињемо са 4000 УСД (приливи готовине на крају 1. године) и бирамо опсег до 22.000 УСД (што одговара приливима готовине у 3. години)

Садашња вредност новчаних токова (1., 2. и 3. година) износи 35.105,3 УСД

Уложени новац или одлив готовине у години 0 износи 20.000 УСД.

Када одбијемо одлив готовине од садашње вредности, добијамо нето садашњу вредност као$15,105.3

НПВ Пример # 2 - са уједначеним приливом готовине

Утврдите нето садашњу вредност пројекта за коју је потребна рана инвестиција вредна 245.000 УСД, док се процењује да ће у наредних 12 месеци долазити у готовини од 40.000 УСД сваког месеца. Преостала вредност пројекта се претпоставља нула. Очекивана стопа поврата је 24% годишње.

НПВ Пример # 2 - Решење коришћењем ручног израчунавања

Дато,

Рана инвестиција = 245.000 УСД

Укупни долазак готовине по периоду = 40.000 УСД

Бројање периода = 12

Попуст за сваки период = 24% / 12 = 2%

Прорачун НПВ:

= $40,000*(1-(1+2%) ^-12)/2% – $245,000

= $178,013.65

НПВ Пример # 2 - Решење помоћу Екцел-а

Као и у претходном примеру, прво што ћемо урадити је да приливе готовине и одливе готовине ставимо у стандардни формат као што је дато у наставку.

У овом примеру треба напоменути неколико важних ствари -

1. У овом примеру пружају нам се месечни приливи готовине, док је дисконтна стопа предвиђена за целу годину.
2. У формули НПВ, морамо осигурати да дисконтна стопа и новчани приливи буду у истој учесталости, што значи да ако имамо месечне новчане токове, онда бисмо требали имати месечну дисконтну стопу.
3. У нашем примеру ћемо заобићи дисконтну стопу и претворити ову годишњу дисконтну стопу у месечну дисконтну стопу.
4. Годишња стопа попуста = 24%. Месечна дисконтна стопа = 24% / 12 = 2%. У својим прорачунима ћемо користити дисконтну стопу од 2%

Користећи ове месечне новчане приливе и месечну дисконтну стопу од 2%, израчунавамо садашњу вредност будућих новчаних токова.

Садашњу вредност месечних прилива готовине добијамо као 423.013,65 УСД

Уложени новац или одлив готовине у 0-ом месецу износио је 245 000 УСД.

Овим добијамо нето садашњу вредност од 178.013,65 УСД

Шта је КСНПВ?

Функција КСНПВ у Екцелу првенствено одређује нето садашњу вредност (НПВ) за низ новчаних плаћања која у суштини не морају бити периодична.

КСНПВ_{т = 1 до Н.} = ∑ Ци / [(1 + Р) д к д_о/365]

Где,

• д_Икс = к’тх датум трошкова
• д_о = датум 0-тог трошка
• Ц._и = и-ти трошак

Коришћење КСНПВ у програму Екцел

Функција КСНПВ у програму Екцел користи следећу формулу за израчунавање нето садашње вредности било које инвестиционе могућности:

КСНПВ (Р, опсег вредности, опсег датума)

Где,

Р = дисконтна стопа за новчане токове

Распон вредности = Скуп нумеричких података који приказују приход и исплате, где:

• Позитивне бројке су идентификоване као приход;
• Негативне цифре се идентификују као плаћања.

Прва исплата је дискрециона и означава плаћање или трошак на почетку инвестиције.

Период = Распон датума еквивалентан низу трошкова. Овај низ плаћања треба да се подудара са низом испоручених вредности.

Пример КСНПВ

Узећемо исти пример који смо узели раније са НПВ и видећемо да ли постоји било каква разлика између два приступа НПВ у односу на КСНПВ.

Претпоставимо да компанија жели да анализира процењену одрживост кључног пројекта који захтева рани одлив од 20.000 долара. Током периода од три године чини се да пројекат доноси приходе од 4000, 14.000 и 22.000 долара, респективно. Предвиђена дисконтна стопа очекује се на 5,5%.

Прво ћемо приливе и одливе готовине ставити у стандардни формат. Овде имајте на уму да смо такође ставили одговарајуће датуме заједно са приливима и одливима готовине.

Други корак је израчунавање пружањем свих потребних уноса за КСНПВ - дисконтне стопе, опсег вредности и распон датума. Приметићете да смо у ову КСНПВ формулу укључили и одливе готовине обављене данас.

Садашњу вредност добијамо помоћу КСНПВ као 16.065,7 долара.

Са НПВ смо добили ову садашњу вредност од 15.105,3 УСД

Садашња вредност која користи КСНПВ већа је од вредности НПВ. Можете ли погодити зашто добијамо различите садашње вредности под НПВ у односу на КСНПВ?

Одговор је једноставан. НПВ претпоставља да се будући приливи готовине дешавају на крају године (од данас). Претпоставимо да је данас 3. јула 2017. године, тада се очекује да ће први новчани прилив од 4000 УСД доћи након годину дана од овог датума. То значи да 3. јула 2018. године добијате 4.000 УСД, 3. јула 2019. године 14.000 УСД, а 3. јула 2020. године 22.000 УСД.

Међутим, када смо израчунали садашњу вредност помоћу КСНПВ, датуми прилива готовине били су стварни датуми на крају године. Када користимо КСНПВ, дисконтујемо први новчани ток за период краћи од једне године. Исто тако и за друге. Резултат тога је да садашња вредност помоћу КСНПВ формуле буде већа од те НПВ формуле.

Пример КСНПВ

Узећемо исти НПВ Пример 2 за решавање помоћу КСНПВ.

Утврдите нето садашњу вредност пројекта за коју је потребна рана инвестиција вредна 245.000 УСД, док се процењује да ће у наредних 12 месеци долазити у готовини од 40.000 УСД сваког месеца. Претпоставља се да је преостала вредност пројекта нула. Очекивана стопа поврата је 24% годишње.

Први корак је прилив и одлив готовине ставити у стандардни формат приказан испод.

У примеру НПВ, претворили смо годишњу дисконтну стопу у месечну дисконтну стопу. За КСНПВ нисмо потребни да урадимо овај додатни корак. Можемо директно користити годишњу дисконтну стопу

Следећи корак је употреба дисконтне стопе, опсега новчаних токова и периода у формули. Имајте на уму да смо у формулу укључили и одливе готовине које смо данас урадили.

Садашња вредност помоћу КСНПВ формуле износи 183.598,2 УСД

За разлику од ове вредности НПВ Формуле, садашња вредност која користи НПВ износи 178.013,65 УСД

Зашто тамо КСНПВ формула даје садашњу вредност већу од вредности НПВ? Одговор је једноставан и остављам вама да у овом случају супротставите НПВ и КСНПВ.

Пример НПВ вс КСНПВ

Узмимо сада још један пример са НПВ наспрам КСНПВ. Претпоставимо да имамо следећи профил новчаног тока

Година одлива готовине - 20.000 УСД

Прилив готовине

• 1. година - 4000 долара
• 2. година - 14.000 долара
• 3. година - 22.000 долара

Циљ овде је сазнати да ли ћете прихватити овај пројекат или одбити овај пројекат с обзиром на низ трошкова капитала или стопа с попустом.

Коришћење НПВ

Трошкови капитала су у крајњој левој колони, почевши од 0% и иду на 110% са кораком од 10%.

Прихватићемо пројекат ако је НПВ већи од 0, иначе ћемо пројект одбити.

Из горњег графикона примећујемо да је НПВ позитивна када су трошкови капитала 0%, 10%, 20% и 30%. То значи да прихватамо пројекат када је цена капитала од 0% до 30%.

Међутим, када се цена капитала повећа на 40%, приметићемо да је нето садашња вредност негативна. Тамо одбацујемо овај пројекат. Примећујемо да како се трошак капитала повећава, нето садашња вредност опада.

То се графички може видети на доњем графикону.

Коришћење КСНПВ

Поведимо сада исти пример са формулом КСНПВ.

Примећујемо да је нето садашња вредност позитивна коришћењем КСНПВ за трошкове капитала од 0%, 10%, 20%, 30% као и 40%. То значи да прихватамо пројекат када је цена капитала између 0% и 40%. Имајте на уму да се овај одговор разликује од одговора који смо добили користећи НПВ где смо одбили пројекат када је цена капитала достигла 40%.

Графикон доле приказује нето садашњу вредност пројекта користећи КСНПВ по различитим трошковима капитала.

Уобичајене грешке за КСНПВ функцију

Ако корисник добије грешку док користи функцију КСНПВ у Екцелу, то може спадати у неку од доле наведених категорија: