Модел попуста на дивиденду (формула, пример) | Водич за ДДМ
Шта је модел попуста на дивиденду?
Модел попуста на дивиденду, познат и као ДДМ, у којем се цена акција израчунава на основу вероватних дивиденди које ће бити исплаћене и које ће бити дисконтоване по очекиваној годишњој стопи. Једноставним речима, то је начин вредновања предузећа заснован на теорији да је акција вредна дисконтоване суме свих будућих исплата дивиденде. Другим речима, користи се за процену залиха на основу нето садашње вредности будућих дивиденди.
Детаљно објашњено
Финансијска теорија наводи да вредност акције вреди све будуће новчане токове за које се очекује да ће их генерирати компанија дисконтована одговарајућом стопом прилагођеном ризику. Дивиденде можемо користити као меру новчаних токова враћених акционару.
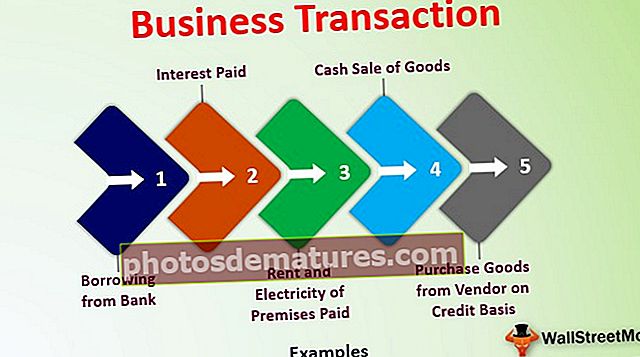
Неки примери редовних компанија које исплаћују дивиденде су МцДоналд’с, Процтер & Гамбле, Кимберли Цларк, ПепсиЦо, 3М, ЦоцаЦола, Јохнсон & Јохнсон, АТ&Т, Валмарт, итд. Можемо да користимо модел попуста на дивиденде да бисмо вредновали ове компаније.

извор: ицхартс
Најважније - преузмите образац модела попуста на дивиденду
Научите процену попуста на дивиденде у програму Екцел
Својствена вредност акције је садашња вредност целог будућег новчаног тока који генеришу акције. На пример, ако купите деоницу и никада не намеравате да је продате (бесконачан временски период). Који су будући новчани токови које ћете добити од ове залихе? Дивиденде, зар не?

Овде је ЦФ = Дивиденда.
Модел попуста на дивиденде одређује цену акције додавањем њених будућих новчаних токова дисконтованих потребном стопом поврата коју инвеститор захтева због ризика поседовања деоница.
Међутим, ова ситуација је помало теоретска, јер инвеститори обично улажу у акције за дивиденде, као и за повећање вредности капитала. Апрецијација капитала је када акцију продате по вишој цени од оне за коју купујете. У таквом случају постоје два новчана тока -
- Будуће исплате дивиденди
- Будућа продајна цена
Пронађите садашње вредности ових новчаних токова и саберите их:
Формула
Модел попуста на дивиденде = унутрашња вредност = зброј садашње вредности дивиденде + садашња вредност продајне цене акција.
Цена овог модела с попустом на дивиденду или ДДМ модела је Суштинска вредност залиха.
Ако акција не исплати дивиденду, тада ће очекивани будући новчани ток бити продајна цена акције. Узмимо пример.
Пример модела попуста на дивиденду
Најважније - преузмите образац модела попуста на дивиденду
Научите процену попуста на дивиденде у програму Екцел
У овом примеру примера дисконтног модела претпоставите да размишљате о куповини деоница која ће следеће године исплатити 20 УСД (Див 1) и 21,6 (Див 2) следеће године. Након добијања друге дивиденде, планирате продају акције по цени од 333,3 долара. Колика је стварна вредност ове залихе ако је ваш захтевани принос 15%?
Решење:
Овај пример модела попуста на дивиденду може се решити у 3 корака -
Корак 1 - Пронађите тренутну вредност дивиденди за 1. годину и 2. годину.
- ПВ (1. година) = 20 УСД / ((1.15) ^ 1)
- ПВ (2. година) = 20 УСД / ((1,15) ^ 2)
- У овом примеру они износе 17,4 и 16,3 долара за дивиденду за прву и другу годину.
Корак 2 - Пронађите тренутну вредност будуће продајне цене након две године.
- ПВ (продајна цена) = 333,3 УСД / (1,15 ^ 2)
Корак 3 - Додајте садашњу вредност дивиденде и садашњу вредност продајне цене
- $17.4 + $16.3 + $252.0 = $285.8

Врсте модела попуста на дивиденде
Сада када смо схватили саму основу модела попуста на дивиденде, кренимо напред и научимо о три врсте модела попуста на дивиденде.
- Модел попуста на дивиденду нултог раста - Овај модел претпоставља да све дивиденде које се плаћају остају заувек једнаке и исте до бесконачности.
- Модел дисконтног дивидендног константног раста - Овај модел дисконтних дивиденди претпоставља да дивиденде расту са фиксним процентом годишње. Они нису променљиви и константни су.
- Модел попуста на варијабилни раст дивиденде или нестални раст - Овај модел може поделити раст у две или три фазе. Прва ће бити брза почетна фаза, затим спорија прелазна фаза, а затим на крају завршава са нижом стопом у бесконачном периоду.
О сваком ћемо сада детаљније разговарати.
# 1 - Модел попуста на дивиденде са нултим растом
Модел нултог раста претпоставља да дивиденда увек остаје иста, тј. Да нема раста дивиденди. Стога би цена акције била једнака годишњим дивидендама подељеним потребном стопом приноса.
Сопствена вредност акције = годишње дивиденде / захтевана стопа поврата
То је у основи иста формула која се користи за израчунавање садашње вредности трајности и може се користити за одређивање цене приоритетне акције, која плаћа дивиденду која је одређени проценат њене номиналне вредности. Акције засноване на моделу нултог раста могу се и даље мењати у цени ако се потребна стопа, на пример, промени када се примети перципирани ризик.
Модел попуста на дивиденду нултог раста - пример
Ако пожељни удео у акцији исплати дивиденду у износу од 1,80 долара годишње, а потребна стопа поврата деоница је 8%, која је онда њена унутрашња вредност?
Решење:
Овде користимо формулу модела дивидендног попуста за дивиденду нултог раста,
Формула модела попуста на дивиденде = унутрашња вредност = годишње дивиденде / потребна стопа поврата
Унутрашња вредност = 1,80 $ / 0,08 = 22,50 УСД.
Недостатак горњег модела је тај што бисте очекивали да ће већина компанија временом расти.
# 2 - ДДМ модел са константним растом
Модел попуста на дивиденде са сталним растом или Гордон модел раста претпоставља да дивиденде расту за одређени проценат сваке године,
Можете ли ценити Гоогле, Амазон, Фацебоок, Твиттер помоћу ове методе? Наравно, не јер ове компаније не дају дивиденде и, што је још важније, расту много бржим темпом. Модели сталног раста могу се користити за вредновање зрелих компанија, чије се дивиденде годинама повећавају.
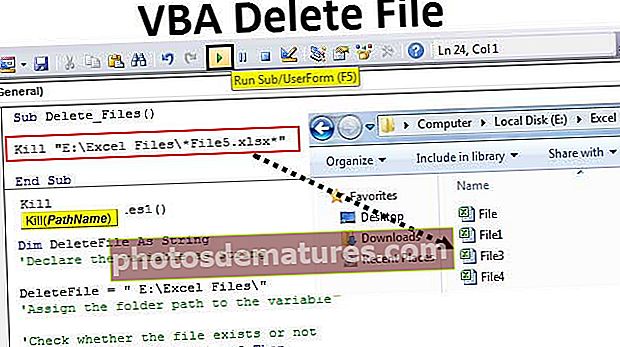
Погледајмо Валмарт-ове дивиденде исплаћене у последњих 30 година. Валмарт је зрела компанија и примећујемо да су се дивиденде непрекидно повећавале током овог периода. Ова компанија може бити кандидат који се може вредновати помоћу модела дисконтних дивиденди са сталним растом.

извор: ицхартс
Имајте на уму да у моделу дисконтних дивиденди са сталним растом претпостављамо да је стопа раста дивиденди константан; Међутим стварни издаци за дивиденде повећавају се сваке године.
Стопе раста дивиденди се обично означавају као г, а потребна стопа означава се са Ке. Још једна важна претпоставка коју бисте требали имати на уму је обавезна стопа или Ке такође остаје константна сваке године.
Стални раст Модел попуста на дивиденде или ДДМ модел даје нам садашњу вредност бесконачног тока дивиденди које расту константном стопом.
Формула дисконтног модела константног раста је доленаведена -

Где:
- Д1 = Вредност дивиденде која ће се добити следеће године
- Д0 = Вредност дивиденде примљене ове године
- г = стопа раста дивиденде
- Ке = дисконтна стопа
Модел дисконтних дивиденди са сталним растом - Пример # 1
Ако акција ове године исплати дивиденду од 4 долара, а дивиденда расте 6% годишње, која ће онда бити стварна вредност акције, под претпоставком да је потребна стопа поврата 12%?
Решење:

Д1 = 4 долара к 1,06 = 4,24 долара
Ке = 12%
Стопа раста или г = 6%
Интерна цена акције = 4,24 УСД / (0,12 - 0,06) = 4 УСД / 0,06 = 70,66 УСД
Модел дисконтних дивиденди са сталним растом - Пример # 2
Ако се акција продаје по цени од 315 долара, а тренутна дивиденда је 20 долара. Шта би могло претпоставити тржиште под претпоставком стопе раста дивиденди за ову акцију ако је стопа захтеваног приноса 15%?
Решење:
У овом примеру ћемо претпоставити да је тржишна цена унутрашња вредност = 315 америчких долара
То подразумева,
315 УСД = 20 УСД к (1 + г) / (0,15 г)
Ако решимо горњу једначину за г, добићемо подразумевана стопа раста од 8,13%
# 3 - ДДМ модел променљиве стопе раста (вишестепени модел попуста на дивиденду)
Модел с попустом на дивиденду са променљивом стопом раста или ДДМ модел много је ближи стварности у поређењу са друге две врсте модела с попустом на дивиденду. Овај модел решава проблеме везане за нестабилне дивиденде претпостављајући да ће компанија доживети различите фазе раста.
Променљиве стопе раста могу имати различите облике; можете чак претпоставити да су стопе раста различите за сваку годину. Међутим, најчешћи облик је онај који претпоставља 3 различите стопе раста:
- почетна висока стопа раста,
- прелазак на спорији раст и
- на крају, одржива, стабилна стопа раста.
Првенствено се проширује модел сталног раста, при чему се свака фаза раста израчунава методом сталног раста, али користећи различите стопе раста за различите фазе. Садашње вредности сваке фазе се сабирају да би се добила унутрашња вредност залиха.
Ово се може применити на следећи начин:
# 3.1 - Двостепени ДДМ
Овај модел је дизајниран да вреднује капитал предузећа, са две фазе раста, почетним периодом већег раста и наредним периодом стабилног раста.
Двостепени модел дисконтних дивиденди; најприкладније за фирме које исплаћују заостали новац у виду дивиденди, а имају умерен раст. На пример, разумније је претпоставити да ће фирма која расте са 12% у периоду високог раста видети да ће њена стопа раста после тога пасти на 6%.
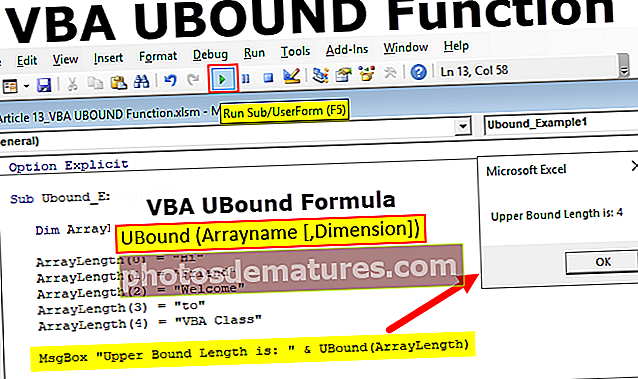
Претпостављам да компаније са већим коефицијентом исплате дивиденде могу одговарати таквом моделу. Као што примећујемо у наставку, такве две компаније - Цоца-Цола и ПепсиЦо. Обе компаније настављају редовно да исплаћују дивиденде, а њихов однос исплате дивиденде је између 70-80%. Поред тога, ове две компаније показују релативно стабилне стопе раста.

извор: ицхартс
Претпоставке
- У првом периоду очекује се већа стопа раста.
- Ова виша стопа раста на крају првог периода ће пасти на стабилну стопу раста.
- Однос исплате дивиденде је у складу са очекиваном стопом раста.
Двостепени ДДМ модел - пример
ЦхецкМате предвиђа да ће његова дивиденда расти на 20% годишње током наредне четири године пре него што се заувек устали на константних 8%. Дивиденда (текућа 2016. година) = 12 УСД; Очекивана стопа поврата = 15%. Колика је сада вредност залиха?
Корак 1: Израчунајте дивиденде за сваку годину док се не постигне стабилна стопа раста
Прва компонента вредности је садашња вредност очекиваних дивиденди током периода високог раста. На основу тренутних дивиденди (12 УСД), очекивана стопа раста (15%) вредности дивиденди (Д1, Д2, Д3) може се израчунати за сваку годину у периоду високог раста.
Стабилна стопа раста постиже се након 4 године. Дакле, израчунавамо профил дивиденде до 2010. године.

Корак 2: Примените модел попуста на дивиденду за израчунавање вредности терминала (цена на крају фазе високог раста)
Модел попуста на дивиденде можемо користити у било ком тренутку. Овде, у овом примеру, раст дивиденде је константан у прве четири године, а затим се смањује, па можемо израчунати цену за коју би акција требало да се прода за четири године, односно коначну вредност на крају високог раста фаза (2020). Ово се може проценити помоћу формуле модела дисконтације константног раста -

Примењујемо формулу модела попуста на дивиденду у екцелу, као што се види доле. Вредност ТВ-а или терминала на крају 2020. године.
Вредност терминала (2020) је 383,9 долара

Корак 3: Пронађите тренутну вредност свих пројектованих дивиденди
Садашња вредност дивиденди током периода високог раста (2017-2020) дата је у наставку. Имајте на уму да је у овом примеру потребна стопа поврата 15%

Корак 4: Пронађите тренутну вредност вредности терминала.
Садашња вредност вредности терминала = 219,5 УСД

Корак 5: Пронађите фер вредност - ПВ пројектованих дивиденди и ПВ терминалне вредности
Као што већ знамо да је унутрашња вредност акције садашња вредност будућих токова готовине. Будући да смо израчунали садашњу вредност дивиденде и садашњу вредност терминалне вредности, укупни збир обе вредности одражаваће фер вредност залиха.
Фер вредност = ПВ (пројектоване дивиденде) + ПВ (терминална вредност)
Фер вредност износи 273,0 УСД

Такође можемо сазнати ефекат промена у очекиваној стопи поврата на фер цену акције. Као што примећујемо из доњег графикона да је очекивана стопа поврата изузетно осетљива на потребну стопу поврата. Треба водити рачуна о потребној стопи поврата. Потребна стопа поврата професионално се израчунава помоћу ЦАПМ модела.

# 3.2 - Трофазни модел попуста на дивиденде ДДМ
Једно од побољшања које можемо направити у двостепеном ДДМ моделу је омогућавање да се стопа раста мења полако, а не тренутно.
Тростепени модел попуста на дивиденде или ДДМ модел дат је према:
- Прва фаза: постоји константан раст дивиденде (г1) или без дивиденде
- Друга фаза: долази до постепеног пада дивиденде до крајњег нивоа
- Трећа фаза: поново постоји константан раст дивиденди (г3), тј. могућности предузећа за раст су готове.
Логика коју смо применили на двостепени модел може се применити и на тростепени модел на сличан начин. Испод је формула модела попуста на дивиденду за примену у три фазе.

Мој савет би био да вас не застрашују ове формуле дивидијског попуста. Само покушајте да примените логику коју смо користили у двостепеном моделу попуста на дивиденду. Једина промена ће бити да ће постојати још једна стопа раста између фазе високог раста и фазе стабилности. За ову стопу раста треба да сазнате одговарајуће дивиденде и њихове садашње вредности.
Ако желите да пронађете још примера залиха које исплаћују дивиденде, можете се позвати на Листу аристократа за дивиденде. Ова листа садржи 50 акција са историјом исплате дивиденди старом од 25 година.
Предности
- Звучна логика - Модел попуста на дивиденду покушава да вреднује залихе на основу свих будућих профила новчаног тока. Овде будући новчани токови нису ништа друго до дивиденде. Поред тога, у математичком моделу је врло мало субјективности, па стога многи аналитичари показују веру у овај модел.
- Матуре Бусинесс - Редовна исплата дивиденде подразумева да је компанија доспела и да можда неће бити велике колебљивости повезане са стопама раста и зарадом. Ово је важно за инвеститоре који више воле да улажу у акције које редовно исплаћују дивиденде.
- Доследност - С обзиром на то да се дивиденде у већини случајева исплаћују у готовини, компаније имају тенденцију да своје исплате дивиденди ускладе са основама пословања. То имплицира да компаније можда неће желети да манипулишу исплатама дивиденди јер оне могу директно довести до волатилности цена акција.
Ограничења
Да бисмо разумели ограничења модела попуста на дивиденде, узмимо пример Берксхире Хатхаваи-а.
Извршни директор Варрен Буффетт напомиње да су дивиденде готово крајње уточиште за корпоративно управљање, предлажући да компаније радије инвестирају у своје пословање и траже „пројекте који ће постати ефикаснији, територијално се проширити, проширити и побољшати производне линије или на други начин проширити економски јарак који раздваја компанија од својих конкурената “. Задржавајући сваки могући долар готовине, Берксхире је могао да га реинвестира са бољим приносима него што би већина акционара сама зарадила.
Амазон, Гоогле, Биоген су други примери који не дају дивиденде и донели су невероватне поврате акционарима.
- Може се користити само за вредновање зрелих компанија - Овај модел ефикасно вреднује компаније које су зреле и не могу да вреднују компаније са високим растом као што су Фацебоок, Твиттер, Амазон и друге.
- Осетљивост претпоставки - Као што смо раније видели, поштена цена је веома осетљива на стопе раста и потребну стопу поврата. Промена од 1 одсто у ово двоје може утицати на процену предузећа за чак 10-20%.
- Можда није повезано са зарадом - У теорији, дивиденде треба довести у корелацију са зарадом компаније. Супротно томе, компаније, међутим, покушавају да одрже стабилну исплату дивиденде уместо променљиве исплате на основу зараде. У многим случајевима компаније су чак позајмљивале новац за исплату дивиденде.
Шта даље?
Ако сте сазнали нешто ново или сте уживали у овом посту с попустом на дивиденду, оставите коментар испод. Јавите ми шта мислите. Пуно хвала и чувајте се. Срећно учење!
Корисни постови
Овај чланак је водич за оно што је модел попуста на дивиденде. Овде ћемо разговарати о типовима модела дивидендног попуста (нулти раст, стални раст и променљиви раст - 2 фазе и 3 фазе), формули модела дивиденде са практичним примерима и студијама случајева.
- Прорачун Гордоновог модела раста
- ЦАПМ Бета
- Водич за процену Алибабе
- Формула вредности терминала <