photosdematures.com

Шта је експоненцијална расподела?

Експоненцијална расподела односи се на непрекидну и константну расподелу вероватноће која се заправо користи за моделирање временског периода који особа треба да сачека пре него што се деси дати догађај и та расподела је континуирани пандан геометријској расподели која је уместо тога различита.

Формула експоненцијалне расподеле

Непрекидна случајна променљива Икс (са параметром скале λ> 0) каже се да има експоненцијалну расподелу само ако се његова функција густине вероватноће може изразити множењем параметра скале са експоненцијалном функцијом минус параметра скале и Икс за све Икс већа или једнака нули, иначе је функција густине вероватноће једнака нули.

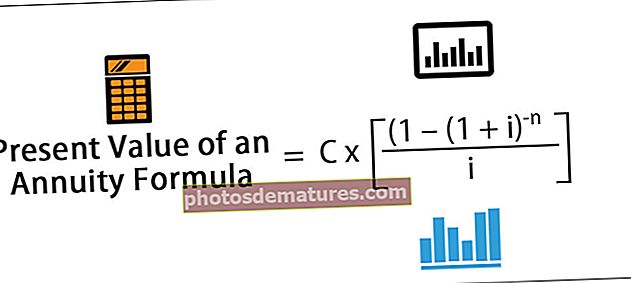
Математички, функција густине вероватноће представљена је као,

такав да је средња вредност једнака 1 / λ, а варијанса једнака 1 / λ2.

Прорачун експоненцијалне расподеле (корак по корак)

• Корак 1: Прво, покушајте да утврдите да ли је разматрани догађај континуиране и независне природе и да ли се дешава отприлике константно. Било који практични догађај осигураће да је променљива већа или једнака нули.
• Корак 2: Затим одредите вредност параметра скале, која је увек реципрочна вредност средње вредности.

• • λ = 1 / средња вредност

• Корак 3: Затим помножите параметар скале λ и променљиву Икс а затим израчунајте експоненцијалну функцију производа помножену са минус један тј. е– λ * к.
• Корак 4: Коначно, функција густине вероватноће израчунава се множењем експоненцијалне функције и параметра скале.

Ако горња формула важи за све Икс веће или једнако нули, онда Икс је експоненцијална расподела.

Пример

Овај Екцел образац за експоненцијалну дистрибуцију можете преузети овде - Екцел образац за експоненцијалну дистрибуцију

Узмимо пример, к који представља количину времена (у минутама) које је канцеларијски службеник одвојио од управниковог стола до службеничког стола. Претпоставља се да узета функција времена има експоненцијалну расподелу са просечном количином времена једнаком пет минута.

С обзиром да Икс је континуирана случајна променљива будући да се време мери.

Просек, μ = 5 минута

Дакле, параметар скале, λ = 1 / μ = 1/5 = 0,20

Дакле, функција вероватноће експоненцијалне расподеле може се извести као,

ф (к) = 0,20 е– 0,20 * к

Сада израчунајте функцију вероватноће при различитим вредностима од Икс да се изведе крива расподеле.

За к = 0

функција вероватноће експоненцијалне расподеле за к = 0 биће,

Слично томе, израчунајте функцију вероватноће експоненцијалне расподеле за к = 1 до к = 30

• За к = 0, ф (0) = 0,20 е -0,20 * 0 = 0,200
• За к = 1, ф (1) = 0,20 е -0,20 * 1 = 0,164
• За к = 2, ф (2) = 0,20 е -0,20 * 2 = 0,134
• За к = 3, ф (3) = 0,20 е -0,20 * 3 = 0,110
• За к = 4, ф (4) = 0,20 е -0,20 * 4 = 0,090
• За к = 5, ф (5) = 0,20 е -0,20 * 5 = 0,074
• За к = 6, ф (6) = 0,20 е -0,20 * 6 = 0,060
• За к = 7, ф (7) = 0,20 е -0,20 * 7 = 0,049
• За к = 8, ф (8) = 0,20 е -0,20 * 8 = 0,040
• За к = 9, ф (9) = 0,20 е -0,20 * 9 = 0,033
• За к = 10, ф (10) = 0,20 е -0,20 * 10 = 0,027
• За к = 11, ф (11) = 0,20 е -0,20 * 11 = 0,022
• За к = 12, ф (12) = 0,20 е -0,20 * 12 = 0,018
• За к = 13, ф (13) = 0,20 е -0,20 * 13 = 0,015
• За к = 14, ф (14) = 0,20 е -0,20 * 14 = 0,012
• За к = 15, ф (15) = 0,20 е -0,20 * 15 = 0,010
• За к = 16, ф (16) = 0,20 е -0,20 * 16 = 0,008
• За к = 17, ф (17) = 0,20 е -0,20 * 17 = 0,007
• За к = 18, ф (18) = 0,20 е -0,20 * 18 = 0,005
• За к = 19, ф (19) = 0,20 е -0,20 * 19 = 0,004
• За к = 20, ф (20) = 0,20 е -0,20 * 20 = 0,004
• За к = 21, ф (21) = 0,20 е -0,20 * 21 = 0,003
• За к = 22, ф (22) = 0,20 е -0,20 * 22 = 0,002
• За к = 23, ф (23) = 0,20 е -0,20 * 23 = 0,002
• За к = 24, ф (24) = 0,20 е -0,20 * 24 = 0,002
• За к = 25, ф (25) = 0,20 е -0,20 * 25 = 0,001
• За к = 26, ф (26) = 0,20 е -0,20 * 26 = 0,001
• За к = 27, ф (27) = 0,20 е -0,20 * 27 = 0,001
• За к = 28, ф (28) = 0,20 е -0,20 * 28 = 0,001
• За к = 29, ф (29) = 0,20 е -0,20 * 29 = 0,001
• За к = 30, ф (30) = 0,20 е -0,20 * 30 = 0,000

Извели смо криву дистрибуције на следећи начин,

Релевантност и употреба

Иако се претпоставка о константној стопи врло ретко задовољава у сценаријима из стварног света, ако је временски интервал одабран на такав начин да је стопа приближно константна, онда се експоненцијална расподела може користити као добар приближни модел. Има много других примена у области физике, хидрологије итд.

У статистици и теорији вероватноће израз експоненцијалне расподеле односи се на расподелу вероватноће која се користи за дефинисање времена између два узастопна догађаја која се дешавају независно и континуирано константном просечном брзином. То је једна од широко коришћених континуираних дистрибуција и строго је повезана са Поиссоновом расподелом у екцелу.