photosdematures.com

Шта је формула вишеструке регресије?

Формула вишеструке регресије користи се у анализи односа између зависних и више независних променљивих, а формула је представљена једначином И је једнако плус бКс1 плус цКс2 плус дКс3 плус Е где је И зависна променљива, Кс1, Кс2, Кс3 су независне променљиве , а је пресјек, б, ц, д су нагиби, а Е је преостала вриједност.

и = мк1 + мк2 + мк3 + б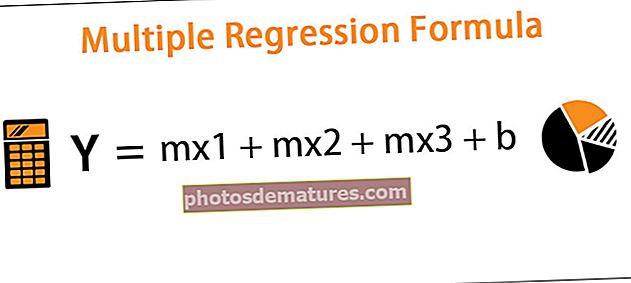

Где,

• И = зависна променљива регресије
• М = нагиб регресије
• Кс1 = прва независна променљива регресије
• Кс2 = друга независна променљива регресије
• Кс3 = трећа независна променљива регресије
• Б = константа

Објашњење формуле регресионе анализе

Вишеструке регресије су метода за предвиђање зависне променљиве уз помоћ две или више независних променљивих. Током извођења ове анализе, главна сврха истраживача је да утврди однос између зависне променљиве и независних променљивих. Да би се предвидела зависна променљива, бира се више независних променљивих које могу помоћи у предвиђању зависне променљиве. Користи се када линеарна регресија није у стању да послужи сврси. Регресијска анализа помаже у процесу валидације да ли су променљиве предиктора довољно добре да помогну у предвиђању зависне променљиве.

Примери

Овде можете преузети овај образац вишеструке регресије формуле Екцел - Екцел образац вишеструке регресије

Пример # 1

Покушајмо да схватимо концепт вишеструке регресионе анализе уз помоћ примера. Покушајмо да откријемо какав је однос између раздаљине коју прелази УБЕР возач и старости возача и броја година искуства возача.

За израчунавање вишеструке регресије идите на картицу Подаци у Екцелу, а затим одаберите опцију анализе података. За даљи поступак и прорачун позива се на дати чланак овде - Аналисис ТоолПак у програму Екцел

Формула регресије за горњи пример биће

1. и = МКС + МКС + б
2. и = 604,17 * -3,18 + 604,17 * -4,06 + 0
3. и = -4377

У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој регресионој једначини је удаљеност коју прелази УБЕР возач, а независне променљиве су старост возача и број искустава која има у вожњи.

Пример # 2

Покушајмо да схватимо концепт вишеструке регресионе анализе уз помоћ другог примера. Покушајмо да откријемо каква је веза између просечног успеха разреда ученика и броја сати учења и висине ученика.

За прорачун идите на картицу Подаци у Екцелу, а затим одаберите опцију анализе података.

Једначина регресије за горњи пример биће

и = МКС + МКС + б

и = 1,08 * .03 + 1,08 * -. 002 + 0

и = .0325

 У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој регресији је ГПА, а независне променљиве су часови студија и висина ученика.

Пример # 3

Покушајмо да схватимо концепт анализе вишеструких регресија уз помоћ другог примера. Покушајмо да откријемо какав је однос између зараде групе запослених у некој организацији и броја година искуства и старости запослених.

За прорачун идите на картицу Подаци у Екцелу, а затим одаберите опцију анализе података.

Једначина регресије за горњи пример биће

• и = МКС + МКС + б
• и = 41308 * .- 71 + 41308 * -824 + 0
• и = -37019

У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој регресионој једначини је плата, а независне променљиве су искуство и старост запослених.

Релевантност и употреба

Вишеструка регресија је врло корисна статистичка метода. Регресија игра веома важну улогу у свету финансија. Много предвиђања се врши помоћу регресионе анализе. На пример, продаја одређеног сегмента може се унапред предвидети уз помоћ макроекономских показатеља који имају врло добру корелацију са тим сегментом.