photosdematures.com

Дефиниција Пеарсоновог коефицијента корелације

Пеарсонов коефицијент корелације, познат и као Пеарсон Р статистички тест, мери снагу између различитих променљивих и њихових односа. Кад год се спроводи било који статистички тест између две променљиве, тада је увек добро да особа која ради анализу израчуна вредност коефицијента корелације како би знала колико је јак однос између две променљиве.

Пеарсонов коефицијент корелације даје вредност између -1 и 1. Интерпретација коефицијента корелације је као у:

• Ако је коефицијент корелације -1, то указује на снажну негативну везу. То подразумева савршени негативни однос између променљивих.
• Ако је коефицијент корелације 0, то значи да нема везе.
• Ако је коефицијент корелације 1, то указује на снажну позитивну везу. То подразумева савршен позитиван однос између променљивих.

Већа апсолутна вредност коефицијента корелације указује на јачи однос између променљивих. Дакле, коефицијент корелације од 0,78 указује на јачу позитивну корелацију у односу на вредност од рецимо 0,36. Слично томе, коефицијент корелације од -0,87 указује на јачу негативну корелацију у односу на коефицијент корелације од рецимо -0,40.

Другим речима, ако је вредност у позитивном опсегу, то показује да је однос између променљивих позитивно повезан и да се обе вредности заједно смањују или повећавају. С друге стране, ако је вредност у негативном опсегу, то показује да је однос између променљивих у корелацији негативно, а обе вредности ће ићи у супротном смеру.

Пеарсонова формула коефицијента корелације

Пеарсонова формула коефицијента корелације је следећа,

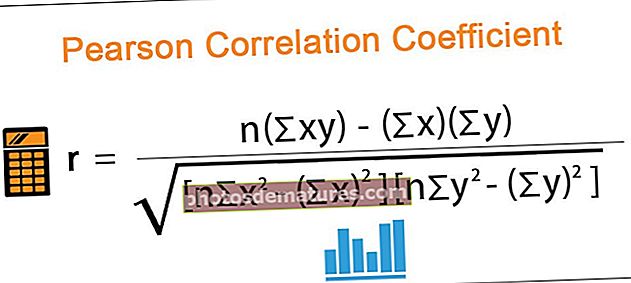
Где,

• р = Пеарсонов коефицијент
• н = број парова залиха
• ∑ки = збир производа упарених залиха
• ∑к = збир к резултата
• ∑и = збир оцена и
• ∑к2 = збир квадратних к резултата
• ∑и2 = зброј квадратних и резултата

Објашњење

Корак 1: Откријте број парова променљивих, који је означен са н. Претпоставимо да се к састоји од 3 променљиве - 6, 8, 10. Претпоставимо да се и састоји од одговарајуће 3 променљиве 12, 10, 20.

Корак 2: Наведите променљиве у две колоне.

Корак 3: У 3. колони сазнајте умножак к и и.

Корак 4: Дознајте збир вредности свих к променљивих и свих и променљивих. Резултате запишите на дну 1. и 2. колоне. У 3. колону упишите збир к * и.

Корак 5: Пронађите к2 и и2 у 4. и 5. колони и њихов збир на дну колона.

Корак 6: Убаците горе пронађене вредности у формулу и решите је.

р = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)

= 0.7559

Пример Пеарсоновог коефицијента корелације Р.

Овај образац Екцел коефицијента корелације Пеарсона можете преузети овде - Предложак Пеарсон коефицијента корелације Екцел

Пример 1

У овом примеру уз помоћ следећих детаља у табели 6 особа различите старости и различитих тежина датих у наставку за израчунавање вредности Пеарсон Р

Решење:

За израчунавање Пеарсоновог коефицијента корелације прво ћемо израчунати следеће вредности,

Овде је укупан број људи 6 па, н = 6

Сада је прорачун Пеарсона Р следећи,

• р = (н (∑ки) - (∑к) (∑и)) / (√ [н ∑к2- (∑к) 2] [н ∑и2– (∑и) 2)
• р = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• р = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• р = (83622- 82618) / (√ [43680 -40804] * [170190- 167281)
• р = 1004 / (√ [2876] * [2909)
• р = 1004 / (√ 8366284)
• р = 1004 / 2892,452938
• р = 0,35

Тако је вредност Пеарсоновог коефицијента корелације 0.35

Пример # 2

Постоје две акције - А и Б. Њихове цене акција одређених дана су следеће:

Из горе наведених података сазнајте Пеарсонов коефицијент корелације.

Решење:

Прво ћемо израчунати следеће вредности.

Израчун Пеарсоновог коефицијента је следећи,

• р = (5*1935-266*37)/((5*14298-(266)^2)*(5*283-(37)^2))^0.5
• = -0.9088

Стога је Пеарсонов коефицијент корелације између две залихе -0,9088.

Предности

• Помаже у сазнању колико је јак однос између две променљиве. Не само присуство или одсуство корелације између две променљиве је назначено коришћењем Пеарсоновог коефицијента корелације, већ такође одређује тачан степен у којој су те променљиве повезане.
• Користећи ову методу, може се утврдити смер корелације, тј. Да ли је корелација између две променљиве негативна или позитивна.

Мане

• Пеарсонов коефицијент корелације Р није довољан да би се утврдила разлика између зависних променљивих и независних променљивих, јер је коефицијент корелације између променљивих симетричан. На пример, ако особа покушава да сазна корелацију између високог стреса и крвног притиска, тада би могла наћи високу вредност корелације која показује да висок стрес узрокује крвни притисак. Ако се променљива промени, резултат ће у том случају бити исти, што показује да стрес узрокује крвни притисак који нема смисла. Дакле, истраживач треба да буде свестан података које користи за спровођење анализе.
• Коришћењем ове методе не може се добити информација о нагибу линије јер се само наводи постоји ли веза између две променљиве или не.
• Вероватно је да се Пеарсонов коефицијент корелације може погрешно протумачити, посебно у случају хомогених података.
• У поређењу са осталим методама израчунавања, овој методи је потребно много времена да би се дошло до резултата.

Важне тачке

• Вредности се могу кретати од вредности +1 до вредности -1, где +1 указује на савршени позитивни однос између разматраних променљивих, -1 указује на савршени негативни однос између разматраних променљивих, а вредност 0 указује на то да ниједан однос постоји између разматраних променљивих.
• Независно је од мерне јединице променљивих. На пример, ако је мерна јединица једне променљиве у годинама, док је мерна јединица друге променљиве у килограмима, чак и тада, вредност овог коефицијента се не мења.
• Коефицијент корелације између променљивих је симетричан, што значи да ће вредност коефицијента корелације између И и Кс или Кс и И остати иста.

Закључак

Пеарсонов коефицијент корелације је врста коефицијента корелације која представља однос између две променљиве које се мере на истом интервалу или на истој скали односа. Он мери снагу односа између две континуалне променљиве.

Не само да наводи присуство или одсуство корелације између две променљиве, већ такође одређује тачну меру у којој су те променљиве повезане. Независно је од мерне јединице променљивих где се вредности коефицијента корелације могу кретати од вредности +1 до вредности -1. Међутим, није довољно рећи разлику између зависних променљивих и независних променљивих.