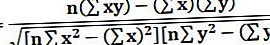photosdematures.com

Дефиниција метода регресије најмањих квадрата

Регресиона метода најмањих квадрата је облик регресионе анализе која успоставља однос између зависне и независне променљиве заједно са линеарном линијом. Ова линија се назива „линија која најбоље одговара“.

Регресиона анализа је статистичка метода помоћу које се могу проценити или предвидети непознате вредности једне променљиве из познатих вредности друге променљиве. Променљива која се користи за предвиђање променљиве камате назива се независном или објашњеном променљивом, а променљива која се предвиђа назива се зависном или објашњеном променљивом.

Размотримо две променљиве к & и. Они се наносе на графикону са вредностима к на вредностима к оси и на и оси. Те вредности су представљене тачкама на доњем графикону. Кроз тачке се повлачи равна линија - која се назива линија која најбоље одговара.

Циљ регресије најмањих квадрата је да се осигура да линија повучена кроз скуп задатих вредности успоставља најближи однос између вредности.

Формула регресије најмањих квадрата

Регресиона линија по методи најмањих квадрата израчунава се помоћу следеће формуле -

ы = а + бк

Где,

• ы = зависна променљива
• к = независна променљива
• а = пресјек и
• б = нагиб линије

Нагиб линије б израчунава се помоћу следеће формуле -

Или

И-пресек, ‘а’ израчунава се помоћу следеће формуле -

Линија најбољег уклапања у најмању квадратну регресију

Линија која најбоље одговара је права линија повучена кроз расуло тачака података која најбоље представља однос између њих.

Размотримо следећи графикон у коме је скуп података уцртан дуж к и и осе. Ове тачке података су представљене помоћу плавих тачака. Кроз ове тачке су повучене три линије - зелена, црвена и плава линија. Зелена линија пролази кроз једну тачку, а црвена линија кроз три тачке података. Међутим, плава линија пролази кроз четири тачке података, а растојање између преосталих тачака до плаве линије је минимално у поређењу са друге две линије.

На горњем графикону, плава линија представља линију која најбоље одговара, јер лежи најближе свим вредностима, а растојање између тачака изван линије до линије је минимално (тј. Растојање између остатака до линије које најбоље одговарају - назива се и сума квадрата остатака). У остале две линије, наранџастој и зеленој, растојање између остатака до линија је веће у поређењу са плавом линијом.

Метода најмањих квадрата пружа најближи однос између зависних и независних променљивих минимизирајући растојање између остатака и линије која најбоље одговара, тј. Зброј квадрата остатака је минималан у овом приступу. Отуда и израз „најмањи квадрати“.

Примери регресионе линије најмање квадрата

Применимо ове формуле у доњем питању -

Овај предложак за регресију најмањих квадрата у Екцелу можете преузети овде - Екцел образац за регресију најмањих квадрата

Пример # 1

Детаљи који се односе на искуство техничара у предузећу (у одређеном броју година) и оцена њиховог учинка дати су у доњој табели. Користећи ове вредности, процените оцену перформанси техничара са 20 година искуства.

Решење -

Да бисмо прво израчунали најмање квадрата, израчунаћемо пресек И (а) и нагиб линије (б) на следећи начин -

Нагиб линије (б)

• б = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1.13

И-пресјек (а)

• а = 648 - (1,13) (80) / 8
• = 69.7

Линија регресије израчунава се на следећи начин -

Заменом вредности к у формули, заменом 20,

• ы = а + бк
• ы = 69,7 + (1,13) (20)
• ы = 92,3

Оцена перформанси техничара са 20 година искуства процењује се на 92,3.

Пример # 2

Једначина регресије најмањих квадрата користећи Екцел

Регресиона једначина најмањих квадрата може се израчунати помоћу екцела у следећим корацима -

• Убаците табелу података у екцел.

• Уметните граф расејања користећи тачке података.

• Уметните линију тренда у графикон расејања.

• Под опцијама линије тренда - изаберите линеарну линију тренда и изаберите једначину приказа на графикону.

• На графикону је приказана једначина регресије најмањих квадрата за дати скуп екцел података.

Тако се израчунава регресиона једначина најмањих квадрата за дати скуп екцел података. Помоћу једначине могу се направити предвиђања и анализе трендова. Екцел алати такође омогућавају детаљна израчунавања регресије.

Предности

• Метода регресионе анализе са најмањим квадратима је најпогоднија за моделе предвиђања и анализу тренда. Најбоље се користи у областима економије, финансија и тржишта акција где се вредност било које будуће променљиве предвиђа уз помоћ постојећих променљивих и однос између истих.
• Метода најмањих квадрата пружа најближи однос између променљивих. Разлика између збира квадрата остатака до линије која најбоље одговара овом методу је минимална.
• Механизам рачунања је једноставан и лак за примену.

Мане

• Метода најмањих квадрата ослања се на успостављање најближе везе између датог скупа променљивих. Механизам израчунавања је осетљив на податке и у случају било каквих одступања (изузетних података) резултати могу углавном утицати.
• Ова врста прорачуна је најприкладнија за линеарне моделе. За нелинеарне једначине примењују се исцрпнији механизми рачунања.

Закључак

Метода најмањих квадрата једна је од најпопуларнијих метода за предвиђање модела и анализу трендова. Када се израчуна на одговарајући начин, доноси најбоље резултате.