photosdematures.com

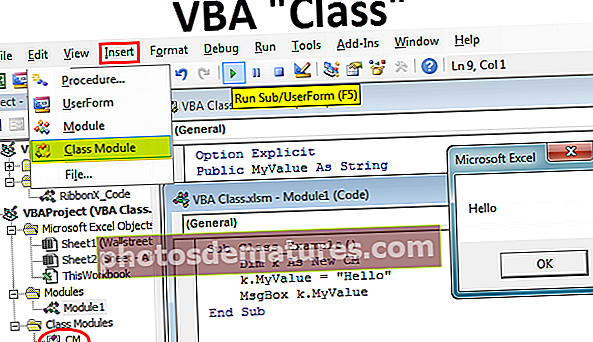
Формула регресионе анализе

Регресијска анализа је анализа односа између зависне и независне променљиве јер приказује како ће се променљива променити када се једна или више независних променљивих промени због фактора, формула за израчунавање је И = а + бКс + Е, где је И зависна променљива, Кс је независна променљива, а је пресек, б је нагиб и Е је остатак.

Регресија је статистички алат за предвиђање зависне променљиве уз помоћ једне или више независних променљивих. Током извођења регресионе анализе, главна сврха истраживача је да утврди однос између зависне променљиве и независне променљиве. Да би се предвидела зависна променљива бира се једна или више независних променљивих које могу помоћи у предвиђању зависне променљиве. Помаже у процесу валидације да ли су променљиве предиктора довољно добре да помогну у предвиђању зависне променљиве.

Формула регресионе анализе покушава да пронађе најбољу линију за зависну променљиву уз помоћ независних променљивих. Једначина регресионе анализе је иста као и једначина за праву која јесте

и = МКС + б

Где,

• И = зависна променљива регресионе једначине
• М = нагиб регресионе једначине
• к = зависна променљива регресионе једначине
• Б = константа једначине

Објашњење

Током регресије, главна сврха истраживача је да утврди однос између зависне променљиве и независне променљиве. Да би се предвидела зависна променљива бира се једна или више независних променљивих које могу помоћи у предвиђању зависне променљиве. Регресијска анализа помаже у процесу валидације да ли су променљиве предиктора довољно добре да помогну у предвиђању зависне променљиве.

Примери

Овај образац за формулу за регресиону анализу Екцел можете преузети овде - Екцел образац за регресиону анализу

Пример # 1

Покушајмо да схватимо концепт регресионе анализе уз помоћ примера. Покушајмо да откријемо какав је однос између удаљености коју је прешао возач камиона и старости возача камиона. Неко у ствари врши регресиону једначину да би потврдио да ли оно што мисли о односу две променљиве валидира и регресиона једначина.

Испод су дати подаци за прорачун

За израчунавање регресионе анализе идите на картицу Подаци у Екцелу, а затим одаберите опцију анализе података. За даљи поступак израчунавања погледајте дати чланак овде - Аналисис ТоолПак у програму Екцел

Формула регресионе анализе за горњи пример биће

• и = МКС + б
• и = 575.754 * -3.121 + 0
• и = -1797

У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој једначини регресије је удаљеност коју пређе возач камиона, а независна променљива је старост возача камиона. Регресија за овај скуп зависних и независних променљивих доказује да је независна променљива добар предиктор зависне променљиве са разумно високим коефицијентом утврђености. Анализа помаже у потврђивању исправности одабира фактора у облику независне променљиве. Снимак испод приказује регресиони излаз за променљиве. Скуп података и променљиве представљени су у приложеном екцел листу.

Пример # 2

Покушајмо да схватимо регресиону анализу уз помоћ другог примера. Покушајмо да откријемо какав је однос између висине ученика одељења и просечне оцене тих ученика. Неко у ствари врши регресиону једначину да би потврдио да ли оно што мисли о односу две променљиве валидира и регресиона једначина.

У овом примеру, испод су дати подаци за израчунавање у екцелу

Израчун регресионе анализе, идите на картицу Подаци у Екцелу, а затим одаберите опцију анализе података.

Регресија за горњи пример биће

• и = МКС + б
• и = 2,65 *, 0034 + 0
• и = 0,009198

У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој једначини регресије је просек успеха ученика, а независна променљива висина ученика. Регресијска анализа за овај скуп зависних и независних променљивих доказује да независна променљива није добар предиктор зависне променљиве јер је вредност коефицијента утврђености занемарљива. У овом случају, морамо да пронађемо другу предикторску променљиву како бисмо предвидели зависну променљиву за регресиону анализу. Снимак испод приказује регресиони излаз за променљиве. Скуп података и променљиве представљени су у приложеном екцел листу.

Релевантност и употреба

Регресија је врло корисна статистичка метода. За сваку пословну одлуку у циљу потврђивања хипотезе да ће одређена акција довести до повећања профитабилности одељења може се потврдити на основу резултата регресије између зависних и независних променљивих. Једначина регресионе анализе игра веома важну улогу у свету финансија. Много предвиђања се врши помоћу регресије. На пример, продаја одређеног сегмента може се унапред предвидети уз помоћ макроекономских показатеља који имају врло добру корелацију са тим сегментом. И линеарна и вишеструка регресија корисне су за практичаре у циљу предвиђања зависних варијабли и валидације независних варијабли као предиктора зависних варијабли.