photosdematures.com

Формула за израчунавање просека

Просек је вредност која се користи за представљање скупа вредности података као што је просек израчунат из целих података и ова формула се израчунава додавањем свих вредности датог скупа, означених са збиром Кс и дељењем са бројем вредности дате у скупу означеним са Н.

Просек = (а₁ + а₂ +…. + а_н) / н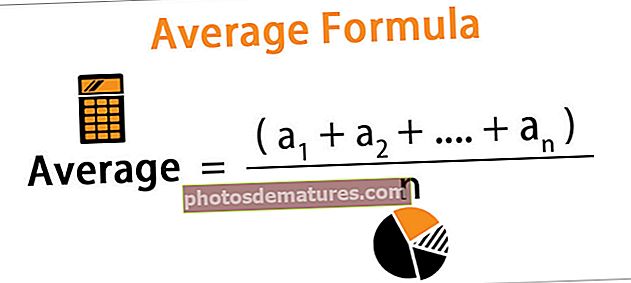

• где_и = и посматрање
• н = Број посматрања

Објашњење

Израчун просека може се израчунати помоћу следећих корака:

• Корак 1: Прво одредите посматрање и они се означавају са а₁, а₂, ... .., а_н што одговара 1. осматрању, 2. запажању,…., н-том посматрању.
• Корак 2: Затим одредите број посматрања и он се означава са н.
• Корак 3: На крају, просек се израчунава додавањем свих запажања, а затим се резултат дели бројем посматрања као што је приказано у наставку.

Просек = (а₁ + а₂ +…. + а_н) / н

Примери

Овај просечни образац формуле Екцел можете преузети овде - просечан образац формуле Екцел

Пример # 1

Узмимо пример Јована који се уписао на дипломски програм за науку о животној средини. Трогодишњи курс је подељен на шест семестара, а коначни просечни проценат израчунава се на основу процената постигнутих у свим семестрима. Израчунајте Јохнов коначни проценат на основу његове следеће оцене:

Испод су дати подаци за израчунавање просечног процента.

Дато,

а₁ = 79%, а₂ = 81%, а₃ = 74%, а₄ = 70%, а₅ = 82%, а₆ = 85%, н = 6

Користећи горње информације, израчун просека биће следећи,

• Просек = (79% + 81% + 74% + 70% + 82% + 85%) / 6

Просек ће бити -

• Просек = 78.50%

Стога је Давид постигао коначни проценат од 78,5% у програму матуре.

Користи

Као што назив „просек“ сугерише, односи се на централну тачку у низу посматрања и када се користи у пољу математике, представља број који је обично средњи за групу бројева. Термин се често користи за изражавање броја који представља групу људи или ствари. Веома је важан, јер помаже у сажимању великог броја података у једну вредност, а такође указује на то да постоји одређена недоследност око једне вредности у оригиналним подацима, што чини веома важан део теорије централних тенденција.