photosdematures.com

Шта је квартилно одступање?

Квартилно одступање заснива се на разлици између првог квартила и трећег квартила у дистрибуцији фреквенције, а разлика је такође позната и као интерквартилни опсег, разлика подељена са два позната је као квартилна девијација или полуинтерквартилни опсег.

Када се узме половина разлике или варијансе између 3. квартила и 1. квартила једноставне расподеле или расподеле фреквенције је квартилно одступање.

Формула

Формула квартилног одступања (К.Д.) користи се у статистици за мерење ширења или другим речима за мерење дисперзије. Ово се такође може назвати полуинтервартилним распоном.

К.Д. = К3 - К1 / 2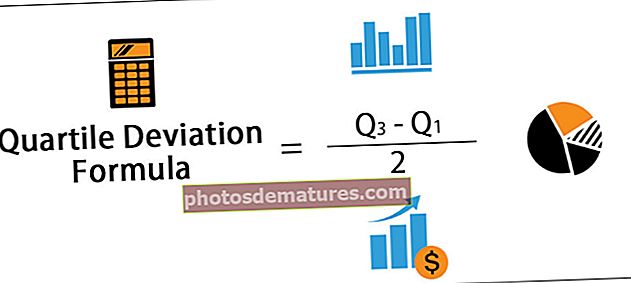

• Формула укључује К3 и К1 у израчун који износи 25%, а смањује 25% података, а када се узме разлика између ове две и када се овај број преполови, то даје мере ширења или дисперзије.
• Дакле, да бисте израчунали квартилно одступање, прво треба да сазнате К1, а затим је други корак пронаћи К3, а затим узети разлику од оба, а последњи корак је поделити са 2.
• Ово је један од најбољих метода дисперзије отворених података.

Примери

Овде можете преузети овај образац Екцел формуле за квартилно одступање - Екцел образац за квартилну девијацију формуле

Пример # 1

Узмите у обзир скуп података следећих бројева: 22, 12, 14, 7, 18, 16, 11, 15, 12. Потребно је да израчунате квартилну девијацију.

Решење:

Прво морамо да поређамо податке у растућем редоследу да бисмо пронашли К3 и К1 и избегли дупликате.

7, 11, 12, 13, 14, 15, 16, 18, 22

Израчун К1 може се извршити на следећи начин,

К1 = ¼ (9 + 1)

=¼ (10)

К1=2.5

Израчун К3 може се извршити на следећи начин,

К3 = ¾ (9 + 1)

=¾ (10)

К3= 7.5 Термин

Израчунавање одступања квартила може се извршити на следећи начин,

• К1 је просек 2. што је 11 и додаје производ разлике између 3. и 4. и 0.5 који је (12-11) * 0.5 = 11.50.
• К3 је седми члан и производ 0,5, а разлика између 8. и 7. члана је (18-16) * 0,5, а резултат је 16 + 1 = 17.

К.Д. = К3 - К1 / 2

Користећи формулу квартилног одступања, имамо (17-11.50) / 2

=5.5/2

К.Д.=2.75.

Пример # 2

Харри лтд. је произвођач текстила и ради на структури награђивања. Управа преговара о покретању нове иницијативе, али прво желе да знају колики је њихов раст производње.

Управа је прикупила своје просечне дневне податке о производњи у последњих 10 дана по (просечном) запосленом.

155, 169, 188, 150, 177, 145, 140, 190, 175, 156.

Користите формулу квартилног одступања како бисте помогли руководству да пронађе дисперзију.

Решење:

Број запажања овде је 10 и наш први корак био би да поређамо податке по узлазном редоследу.

140, 145, 150, 155, 156, 169, 175, 177, 188, 190

Израчун К1 може се извршити на следећи начин,

К1 = ¼ (н + 1) тх члан

=¼ (10+1)

=¼ (11)

К1= 2.75. Термин

Израчун К3 може се извршити на следећи начин,

К3 = ¾ (н + 1) тх члан

=¾ (11)

К3= 8.25 Термин

Израчунавање одступања квартила може се извршити на следећи начин,

• Други члан је 145, а сада се томе додаје 0,75 * (150 - 145), што је 3,75, а резултат 148,75
• Осми термин је 177 и сада се томе додаје 0,25 * (188 - 177) што је 2,75 и резултат је 179,75

К.Д. = К3 - К1 / 2

Користећи формулу квартилног одступања, имамо (179,75-148,75) / 2

=31/2

К.Д.=15.50.

Пример # 3

Рајанова међународна академија жели да анализира колики је проценат бодова њихових ученика раширен.

Подаци су за 25 ученика.

Користите формулу квартилног одступања да бисте сазнали дисперзију у% ознака.

Решење:

Број запажања овде је 25 и наш први корак био би сређивање података у растућем редоследу.

Израчун К1 може се извршити на следећи начин,

К1 = ¼ (н + 1) тх члан

=¼ (25+1)

=¼ (26)

К1= 6.5. Мандат

Израчун К3 може се извршити на следећи начин,

К3 = ¾ (н + 1) тх члан

=¾ (26)

К3 = 19.50 Термин

Израчунавање квартилне девијације или полуинтерквартилног опсега може се извршити на следећи начин,

• Шести термин је 154, а сада се томе додаје 0,50 * (156 - 154), што је 1, а резултат је 155,00
• 19. термин је 177 и сада се томе додаје 0,50 * (177 - 177) што је 0, а резултат је 177

К.Д. = К3 - К1 / 2

Користећи формулу квартилног одступања, имамо (177-155) / 2

=22/2

К.Д.= 11.

Пример # 4

Одредимо сада вредност кроз екцел образац за Практични пример И.

Решење:

За израчунавање одступања квартила користите следеће податке.

Израчун К1 може се извршити на следећи начин,

К1=148.75

Израчун К3 може се извршити на следећи начин,

К3= 179.75

Израчунавање одступања квартила може се извршити на следећи начин,

Користећи формулу квартилног одступања, имамо (179,75-148,75) / 2

К.Д. биће -

КД = 15.50

Релевантност и употреба

Квартилна девијација која је такође позната као полуинтерквартилни опсег. Опет, разлика варијансе између 3. и 1. квартила назива се интерквартилним распоном. Интерквартилни опсег приказује у којој мери су запажања или вредности датог скупа података раширене од средње вредности или њиховог просека. Квартилно одступање или полуинтерквартилни опсег је већина која се користи у случају када неко жели да научи или каже студију о распршености запажања или узорака датих скупова података који леже у главном или средњем делу дате серије. Овај случај би се обично догодио у расподели где подаци или запажања теже да леже интензивно у главном делу или средини датог скупа података или низа, а расподела или вредности не леже ка крајностима, а ако леже тада нису од великог значаја за прорачун.