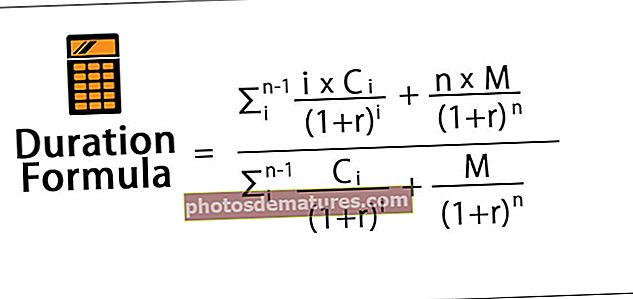photosdematures.com

Шта је формула трајања?

Формула трајања је мера осетљивости обвезнице на промене каматне стопе и израчунава се дељењем збира умножка дисконтованог будућег новчаног прилива обвезнице и одговарајућег броја година са збиром дисконтованог будућег прилива готовине. Прилив готовине у основи се састоји од исплате купона и доспећа на крају. Такође је познато и као трајање Мацаулаи-а.

Математички, једначина трајања је представљена као доле,

где,

• Ц = Исплата купона по периоду
• М = номинална или номинална вредност
• р = ефективна периодична каматна стопа
• н = Број периода до доспећа

Даље, називник који је збир дисконтованог новчаног прилива обвезнице еквивалентан је садашњој вредности или цени обвезнице. Стога се формула за трајање може даље поједноставити као доле,

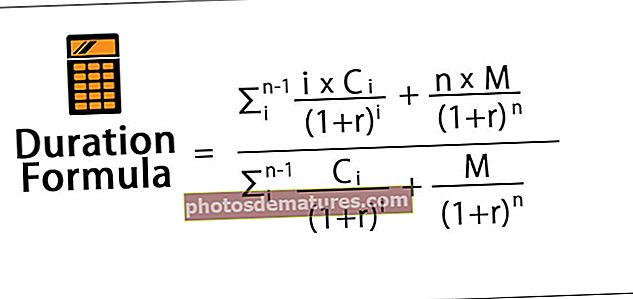
Објашњење формуле трајања

Једначина трајања може се израчунати помоћу следећих корака:

Корак 1: Прво се утврђује номинална или номинална вредност емисије обвезница и означава је М.

Корак 2: Сада се купонска исплата обвезнице израчунава на основу ефективне периодичне стопе камате. Тада се утврђује и учесталост исплате купона. Купонска уплата означена је са Ц, а ефективна периодична каматна стопа са р.

Корак 3: Сада се укупан број периода до доспећа рачуна множењем броја година до доспећа и учесталости уплата купона у години. Број периода до доспећа означава се са н. Такође, бележи се време периодичног плаћања које се означава са и.

Корак 4: Коначно, на основу доступних информација може се извести једначина за време трајања, како следи,

Примери формуле трајања (са Екцел предлошком)

Погледајмо неке једноставне до напредне типове формула трајања да бисмо их боље разумели.

Овај образац за трајање формуле за Екцел можете преузети овде - образац за трајање за формулу за Екцел

Трајање Формула Формула - Пример # 1

Узмимо пример обвезнице са годишњим купонским уплатама. Претпоставимо да је компанија КСИЗ Лтд издала обвезницу номиналне вредности 100.000 америчких долара са годишњом стопом купона од 7% и доспећем за 5 година. Превладавајућа тржишна каматна стопа је 10%.

С обзиром на то, М = 100.000 УСД

• Ц = 7% * 100.000 УСД = 7.000 УСД
• н = 5
• р = 10%

Умањеник или цена обвезнице израчунава се помоћу формуле као,

• Цена обвезнице = 84.281,19

Израчун бројника формуле Трајање је следећи -

= (6,363.64 + 11,570.25 + 15,777.61 + 19,124.38 + 310,460.70)

= 363,296.50

Према томе, израчун трајања везе биће следећи,

Трајање = 363.296,50 / 84.281,19

• Трајање = 4,31 године

Трајање Формула Формула - Пример # 2

Узмимо пример обвезнице са годишњим купонским уплатама. Претпоставимо да је компанија КСИЗ Лтд издала обвезницу чија је номинална вредност 100 000 УСД и која доспева за 4 године. Преовлађујућа тржишна каматна стопа износи 10%. Израчунајте трајање обвезнице за следећу годишњу стопу купона: (а) 8% (б) 6% (ц) 4%

С обзиром на то, М = 100.000 УСД

• н = 4
• р = 10%

Обрачун за стопу купона од 8%

Купонска уплата (Ц) = 8% * 100.000 УСД = 8.000 УСД

Умањеник или цена обвезнице израчунава се помоћу формуле као,

• Цена обвезнице = 88.196,16

Израчун бројила формуле Трајање биће следећи -

= 311,732.8

Према томе, израчун трајања везе биће следећи,

Трајање = 311.732,81 / 88.196,16

• Трајање = 3,53 године

Обрачун за стопу купона од 6%

Купонска уплата (Ц) = 6% * 100.000 УСД = 6.000 УСД

Умањеник или цена обвезнице израчунава се помоћу формуле као,

• Цена обвезнице = 83.222,46

Израчун бројила формуле Трајање биће следећи -

= 302,100.95

Према томе, израчун трајања везе биће следећи,

Трајање = 302.100,95 / 83.222,46

• Трајање = 63 године

Обрачун за стопу купона од 4%

Уплата купона = 4% * 100.000 УСД = 4.000 УСД

Умањеник или цена обвезнице израчунава се помоћу формуле као,

• Цена обвезнице = 78.248,75

Израчун бројила формуле Трајање биће следећи -

= 292,469.09

Према томе, израчун трајања везе биће следећи,

Формула трајања = 292.469,09 / 78.248,75

• Трајање = 3,74 године

Из примера се види да се трајање обвезнице повећава са смањењем стопе купона.

Релевантност и употреба формуле трајања

Важно је разумети концепт трајања јер га инвеститори у обвезнице користе за проверу осетљивости обвезнице на промене каматних стопа. Трајање обвезнице у основи указује на то колико ће се променити тржишна цена обвезнице услед промене каматне стопе. Вреди се напоменути да се каматна стопа и цена обвезница крећу у супротним смеровима и као такве цене обвезница расту када каматна стопа пада и обрнуто.

У случају да инвеститори траже корист од пада каматне стопе, инвеститори ће намеравати да купе обвезнице са дужим роком трајања, што је могуће у случају обвезница са нижом купонском уплатом и дугим роком доспећа. С друге стране, од инвеститора који желе да избегну колебљивост каматних стопа, од инвеститора ће се тражити да улажу у обвезнице краћег рока трајања или кратког рока доспећа и веће исплате купона.