З Формула теста у статистици | Израчун корак по корак (примери)

Формула за израчунавање З теста у статистици

З Тест у статистици односи се на тест хипотезе који се користи да би се утврдило да ли су израчуната средства за два узорка различита, у случају да су доступна стандардна одступања и да је узорак велик.

З = (к - μ) / о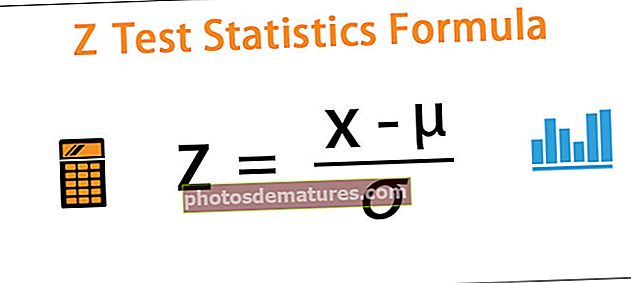

где је к = било која вредност из популације

μ = средња вредност становништва
о = стандардна девијација становништва

У случају узорка, формула за з-тест статистике вредности израчунава се одузимањем средње вредности узорка од к вредности, а затим се резултат дели стандардном девијацијом узорка. Математички је представљен као,

З = (к - к_значи) / с

где

к = било која вредност из узорка
к_меан = средња вредност узорка
с = стандардна девијација узорка

З Израчун теста (корак по корак)

Формула за статистику з-теста за популацију изведена је коришћењем следећих корака:

Корак 1: Прво, израчунајте средњу вредност популације и стандардну девијацију популације на основу посматрања забележеног у средњој вредности популације, а свако посматрање се означава са к_и. Укупан број посматрања у популацији означава Н.

Средња популација,

Стандардна девијација становништва,

Корак 2: На крају, статистика з-теста израчунава се одузимањем средње вредности популације од променљиве, а затим се резултат дели стандардном девијацијом популације као што је приказано доле.

З = (к - μ) / о

Формула за з-тест статистике за узорак изведена је коришћењем следећих корака:

Корак 1: Прво, израчунајте средњу вредност узорка и стандардну девијацију узорка исто као горе. Овде се укупан број запажања у узорку означава са н тако да је н <Н.

Пример узорка,

Узорак стандардне девијације,

Корак 2: На крају, статистика з-теста израчунава се одузимањем средње вредности узорка од к вредности, а затим се резултат дели стандардном девијацијом узорка, као што је приказано доле.

З = (к - к_значи) / с

Примери

Овде можете преузети овај З Тест Формула Екцел предложак - З Тест Формула Екцел Предложак

Пример # 1

Претпоставимо да се популација ученика у школи појавила на разредном тесту. Средња оцена у тесту је 75, а стандардна девијација је 15. Одредите з-тест оцену Давида који је постигао 90 на тесту.

Дато,

Средња насељеност, μ = 75
Стандардна девијација становништва, о = 15

Стога се статистика з-теста може израчунати као,

З = (90 - 75) / 15

З Статистика теста биће -

З = 1

Према томе, Давидов тест резултат је једна стандардна девијација изнад средњег резултата популације, тј. Према табели з-скорова, 84,13% ученика мање бодова од Давида.

Пример # 2

Узмимо пример 30 ученика који су изабрани као део узорка тима који ће бити анкетиран како би се видело колико оловака се користило недељно. Одредите резултат з-теста за 3. ученика на основу датих одговора: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Дато,

к = 5, јер је одговор 3. ученика 5
Величина узорка, н = 30

Средња вредност узорка, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Просек = 4,17

Сада се стандардна девијација узорка може израчунати помоћу горње формуле.

о = 1,90

Стога се резултат з-теста за 3. ученика може израчунати као,

З = (к - к) / с

З = (5-17) / 1,90
З = 0,44

Према томе, употреба трећег ученика је 0,44 пута већа од стандардне девијације изнад средње употребе узорка, тј. Према табели з-сцоре, 67% ученика користи мање оловака од трећег ученика.

Пример # 3

Испод су дати подаци за израчунавање З тестова статистике

За детаљан прорачун З тестова статистике можете се позвати на дати Екцел лист испод.

Релевантност и употреба

Веома је важно разумети концепт статистике з-теста, јер се он обично користи кад год је дискутабилно да ли статистика теста следи нормалну расподелу према дотичној нултој хипотези. Међутим, треба имати на уму да се з-тест користи само када је величина узорка већа од 30, у супротном се користи т-тест.

photosdematures.com