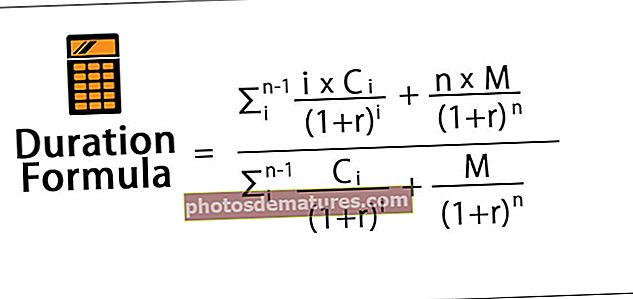photosdematures.com

Формула за израчунавање регресије

Формула регресије користи се за процену односа између зависне и независне променљиве и откривање како утиче на зависну променљиву на промену независне променљиве и представљена једначином И једнако је аКс плус б где је И зависна променљива, а је нагиб регресионе једначине к је независна променљива, а б константа.

Регресијска анализа широко је користила статистичке методе за процену односа између једне или више независних променљивих и зависних променљивих. Регресија је моћно средство, јер се користи за процену снаге односа између две или више променљивих, а затим би се користила за моделирање односа између тих променљивих у будућности.

И = а + бКс + ∈

Где:

• И - је зависна променљива
• Кс - је независна (објашњења) променљива
• а - је пресретање
• б - је нагиб
• ∈ - и је остатак (грешка)

Формула за пресјек „а“ и нагиб „б“ могу се израчунати према доље.

а = (Σи) (Σк2) - (Σк) (Σки) / н (Σк2) - (Σк) 2б = н (Σки) - (Σк) (Σи) / н (Σк2) - (Σк) 2

Објашњење

Регресиона анализа, као што је раније поменуто, углавном се користи за проналажење једначина које одговарају подацима. Линеарна анализа је једна врста регресионе анализе. Једначина за праву је и = а + бКс. И је зависна променљива у формули која покушава да предвиди која ће бити будућа вредност ако се Кс независна променљива промени за одређену вредност. „А“ у формули је пресек који је она вредност која ће остати фиксна без обзира на промене независне променљиве, а израз „б“ у формули је нагиб који означава колика је променљива зависна променљива од независне променљиве.

Примери

Овај образац за регресијску формулу Екцел можете преузети овде - Екцел образац за регресиону формулу

Пример # 1

Узмите у обзир следеће две променљиве к и и, од вас се захтева да извршите прорачун регресије.

Решење:

Користећи горњу формулу, израчунавање линеарне регресије у екцелу можемо извршити на следећи начин.

Имамо све вредности у горњој табели са н = 5.

Сада прво израчунајте пресек и нагиб за регресију.

Израчун пресретања је следећи,

а = (628,33 * 88,017,46) - (519,89 * 106.206,14) / 5 * 88,017,46 - (519,89) 2

а = 0,52

Израчун нагиба је следећи,

б = (5 * 106.206,14) - (519,89 * 628,33) / (5 * 88,017,46) - (519,89) 2

б = 1,20

Унесите сада вредности у формулу регресије да бисмо добили регресију.

Отуда и линија регресије И = 0,52 + 1,20 * Кс

Пример # 2

Индијска државна банка недавно је успоставила нову политику повезивања каматне стопе на штедни рачун са Репо стопом, а ревизор индијске државне банке жели да спроведе независну анализу одлука које је банка донела у вези са променама каматних стопа без обзира да ли су то промене кад год дошло је до промена у стопи Репо. Следи резиме репо стопе и каматне стопе штедних рачуна банке који су владали тих месеци и дати су у наставку.

Ревизор државне банке вам се обратио да извршите анализу и на следећем састанку одржите презентацију о истој. Користите регресиону формулу и утврдите да ли се курс Банке променио како и када је промењена Репо стопа?

Решење:

Користећи горе разматрану формулу, можемо извршити прорачун линеарне регресије у екцелу. Третирање репо стопе као независне променљиве тј. Кс и третирање стопе банке као зависне променљиве као И.

Имамо све вредности у горњој табели са н = 6.

Сада прво израчунајте пресек и нагиб за регресију.

Израчун пресретања је следећи,

а = (24,17 * 237,69) - (37,75 * 152,06) / 6 * 237,69 - (37,75) 2

а = 4,28

Израчун нагиба је следећи,

б = (6 * 152,06) - (37,75 * 24,17) / 6 * 237,69 - (37,75) 2

б = -0,04

Унесите сада вредности у формулу да бисмо дошли до слике.

Отуда и линија регресије И = 4,28 - 0,04 * Кс

Анализа: Чини се да државна банка Индије заиста следи правило повезивања своје стопе штедње са репо стопом, јер постоји нека вредност нагиба која сигнализира везу између репо стопе и стопе штедног рачуна банке.

Пример # 3

Лабораторија АБЦ спроводи истраживање висине и тежине и желела је да зна да ли постоји нека веза попут повећања висине, а такође ће се повећати. Окупили су узорак од 1000 људи за сваку од категорија и дошли до просечне висине у тој групи.

Испод су детаљи које су прикупили.

Од вас се тражи да извршите прорачун регресије и извучете закључак да постоји било какав такав однос.

Решење:

Користећи горе разматрану формулу, можемо извршити прорачун линеарне регресије у екцелу. Третирање висине као независне променљиве тј. Кс и третирање тежине као зависне променљиве као И.

Имамо све вредности у горњој табели са н = 6

Сада прво израчунајте пресек и нагиб за регресију.

Израчун пресретања је следећи,

а = (350 * 120.834) - (850 * 49.553) / 6 * 120.834 - (850) 2

а = 68,63

Израчун нагиба је следећи,

б = (6 * 49.553) - (850 * 350) / 6 * 120.834 - (850) 2

б = -0,07

Унесите сада вредности у формулу да бисмо дошли до слике.

Отуда и линија регресије И = 68,63 - 0,07 * Кс

Анализа: Чини се да постоји знатно мањи однос између висине и тежине, јер је нагиб врло низак.

Релевантност и употреба регресионе формуле

Када коефицијент корелације приказује да подаци могу предвидети будуће исходе, а заједно са тим да се дијаграм расејања истог скупа података чини линеарном или правом линијом, тада се може користити једноставна линеарна регресија користећи најбоље прилагођено проналажење предиктивног вредност или предиктивна функција. Регресиона анализа има много примена у области финансија, као што је коришћена у ЦАПМ-у, који је модел одређивања цена капиталне имовине метода у финансијама. Може се користити за предвиђање прихода и трошкова фирме.