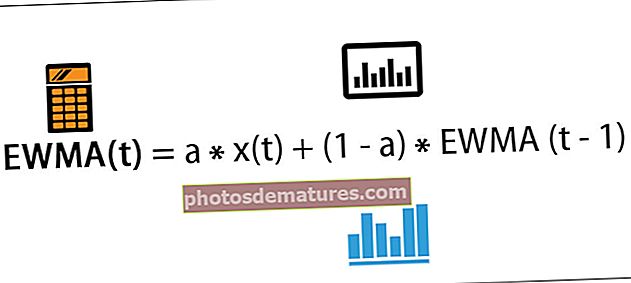photosdematures.com

Шта су факторски модели?

Факторски модели су финансијски модели који укључују факторе (макроекономске, основне и статистичке) за одређивање тржишне равнотеже и израчунавање потребне стопе приноса. Такви модели повезују повраћај хартије од вредности појединачним или вишеструким факторима ризика у линеарном моделу и могу се користити као алтернативе модерној теорији портфеља.

Испод су неке од функција које се односе на факторске моделе

• Максимизација вишка приноса, тј. Алфа (α) (о чему ће бити речи у каснијем делу овог чланка) портфеља;
• Минимизација волатилности портфеља, тј. Бета (β) портфеља;
• Осигурајте довољну диверзификацију да бисте поништили ризик специфичан за предузеће.

Врсте модела фактора

Постоје првенствено две врсте -

1. Појединачни фактор
2. Вишеструки фактор

# 1 - Модел са једним фактором

Најчешћа примена овог модела је модел одређивања цена капиталних средстава (ЦАПМ).

ЦАПМ је модел који прецизно саопштава однос између систематског ризика и очекиваног поврата залиха. Израчунава потребни принос на основу мерења ризика. Да би се то постигло, ослања се на мултипликатор ризика који се назива Бета коефицијент (β).

Овај образац Екцел Фацтор Моделс можете преузети овде - Екцел Темплате Фацтор Моделс

Формула / структура

Е (Р)_и = Р._ф+ β (Е (Р_м) - Р._ф)

Где Е (Р)_Ја је Очекивани повраћај улагања

• Р._ф је дефинисана стопа без приноса без ризика теоријска стопа поврата са нула ризика.
• β је Бета инвестиције која представља колебљивост инвестиције у поређењу са укупним тржиштем
• Е (Р._м) је Очекивани повратак на тржиште.
• Е (Р._м) - Р._ф је премија за тржишни ризик.

Пример

Размотрите следећи пример:

Бета одређене акције је 2. Повратак на тржиште је 8%, а стопа без ризика 4%.

Очекивани повратак према горњој формули био би:

• Очекивани повратак Е (Р)_и= 4+2(8-4)
• = 12%

ЦАПМ је једноставан модел и најчешће се користи у финансијској индустрији. Користи се у израчуну пондерисаних просечних трошкова капитала / трошкова капитала.

Али овај модел заснован је на неколико помало неразумних претпоставки као што је „што је ризичнија инвестиција, то је већи поврат“, што можда не мора бити тачно у свим сценаријима, претпоставка да историјски подаци тачно предвиђају будуће перформансе имовине / залиха итд.

А шта ако постоји много фактора, а не само један који одређује стопу поврата? Стога прелазимо на финансијске моделе и детаљно расправљамо о таквим моделима.

# 2 - Модел вишеструких фактора

Вишефакторски модели су додаци појединачним финансијским моделима. Теорија одређивања арбитражног поступка је једна од његових претежних примена.

Формула / структура

Р._{с, т} = Р._ф + α + β₁× Ф_{1, т} + β₂× Ф_{2, т} + β₃× Ф_{3, т}+ …… .β_н× Ф_{н, т}+ Е

Где Р._{с, т} је повраћај осигурања с у време т

• Р._ф је безризична стопа поврата
• α је Алфа сигурности -Алфа је стални појам фактор фактора. Представља вишак поврата инвестиције у односу на принос референтног индекса. То је вредност за коју инвестиција надмашује индекс. Што је већа алфа, то је боље за инвеститоре
• Ф_{1, т}, Ф._{2, т}, Ф._{3, т} су фактори - макроекономски фактори попут девизног курса, стопе инфлације, страних институционалних инвеститора, БДП, итд. Основни фактори П / Е однос, тржишна капитализација итд.
• β₁, β₂, β₃су факторска оптерећења. - Факторска оптерећења, позната и као компонентна оптерећења, коефицијенти су фактора, као што је горе поменуто. На пример, израчунавање Бета помаже инвеститорима да анализирају величину којом се акција креће у односу на промене на тржишту.
• Е представља термин грешке - Једначина садржи термин грешке који се користи за даљу прецизност израчуна. Понекад се може користити за дефинисање вести о безбедности које постају доступне инвеститорима.

Пример

Размотрите следећи пример:

Претпоставимо да је стопа поврата без ризика 4%.

Повратак израчунат за горњи пример је следећи:

• Р = Р_ф + β₁× Ф_{1, т} + β₂× Ф_{2, т} + Е
• = 4% + 0.6(5) + 0.54(8)
• = 11.32%

Теорија арбитражног одређивања цена, која је један од уобичајених типова финансијских модела, заснива се на следећим претпоставкама:

• Повраћај имовине може се описати линеарним факторским моделом
• Ризик специфичан за имовину / предузеће биће могуће елиминисати диверзификацијом.
• Не постоје даље могућности арбитраже.

Предности

Овај модел омогућава професионалцима

• Разумевање изложености ризику капитала, фиксног дохотка и осталих класа имовине.
• Уверите се да агрегатни портфељ инвеститора испуњава његове апетите за ризиком и очекивањима за повраћајем.
• Направите портфеље који дају конзистентни резултат или преправите у складу са карактеристикама одређеног индекса.
• Процените трошкове сопственог капитала за процену
• Управљајте ризиком и заштитом.

Мане / Ограничења

• Тешко је одлучити колико фактора треба укључити у модел.
• Тумачење значења фактора је субјективно.
• Одабир доброг скупа питања је сложен, а различити истраживачи ће одабрати различите скупове питања.
• Неправилна истрага може довести до компликованих исхода.