Просек у односу на пондерисани просек | 4 најбоље разлике (са Инфографиком)
Просек и пондерисани просек су два различита појма у Екцелу, просек је метода за израчунавање централне тачке датог скупа података и израчунава се традиционални начин израчунавања просека сабирања бројева подељених са бројем присутних скупова података, док пондерисани просек је просек који се израчунава на исти начин, али са тежином помноженом са сваким скупом података.
Разлика између просека и пондерисаног просека
Просек у односу на пондерисани просек је математички и статистички појам у финансијама и послу, али се оба рачунају различито. Просек је збир свих појединачних запажања подељен бројем посматрања. У основи просек који се користи за проналажење средње вредности у одређеном скупу података. Такође је позната и као централна тенденција и користи се за проналажење централне тенденције групе података у одређеној групи података. Пондерисани просек користи се у пољу рачуноводства. А његова главна сврха је пронаћи праву тежину или вредност за решавање. Пондерисани просек је вредност отплате главнице одређених обвезница или зајмова док се главница не исплати.
Шта је просек?
Просек је збир свих појединачних запажања подељен бројем посматрања. У основи, користи се за проналажење средње вредности у одређеном скупу података. Такође је позната и као централна тенденција и користи се за проналажење централне тенденције групе података у одређеној групи података. Углавном се користи за представљање података. То се може решити за скуп података помоћу аритметичке формуле.
Просечна формула = Збир посматрања / Број посматрања
Пример просека
Погледајмо пример за разумевање просека.
Претпоставимо да у разреду има 10 ученика са оценама 50, 60, 70, 80, 65, 78, 95, 63, 58, 91, односно од 100, сада ћемо наћи просек за изнад оцене ученика. Као што знамо.
Просечна формула = Збир посматрања / Број посматрања
Збир посматрања = 50 + 60 + 70 + 80 + 65 + 78 + 95 + 63 + 58 + 9
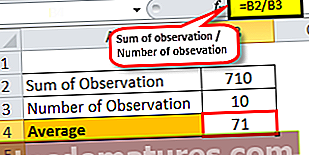
Дакле, просек одељења од 10 ученика је 71.

Шта је пондерисани просек?
Пондерисани просек користи се у пољу рачуноводства. Његова главна сврха је пронаћи праву тежину или вредност за решавање. Пондерисани просек је вредност отплате главнице одређених обвезница или зајмова док се главница не исплати. Пондерисани просек је такође врста просека са малом разликом, јер сва посматрања немају једнаке тежине, различита посматрања имају различиту важност, свако посматрање се помножи са тежином и сабере. За извођење се користи просек тежине. Може се узети као просек у коме свака вредност има различиту тежину. И на то утиче тежина вредности података. Пондерисана вредност је збир производа запажања на тежину подељену са збиром тежине и може се записати као: -
Пондерисана просечна формула = (а1в1 + а2в2 + а3в3 +… + анвн) / (в1 + в2 + в3… + вн)
Пример пондерисаног просека
Погледајмо пример како бисмо га боље разумели.
Претпоставимо да постоје три различита испита која доприносе давању коначних оцена за годину дана и да је различита тежина сваког испита за тежину првог испита била 15%, за другу тежину 25% и за коначну тежину 60%. студент је на првом испиту постигао 60 оцена, на другом 70 и на завршном испиту 80 од 100, израчунајмо сада коначне оцене ученика.
За његово израчунавање користите горе поменуту формулу.
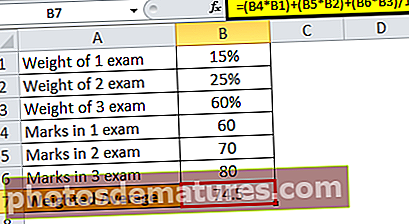
- Дакле, пондерисани просек ученика је 74,5.
Просек у односу на пондерисани просек Инфографике
Овде вам пружамо првих 5 разлика.
Просек у односу на пондерисани просек - кључне разлике
Кључне разлике између овог просека су следеће -
- Просек је збир свих појединачних запажања подељен бројем посматрања, док је пондерисани просек посматрање помножено са тежином и сабрано да би се пронашло решење.
- Просек је математичка једначина, док се пондерисани просек примењује у свакодневним финансијским активностима.
- Просек је приказ скупа података, док пондерисани просек треба проценити да би се дошло до решења проблема.
- Просек се може решити за скуп података помоћу аритметичке формуле, а пондерисаној компоненти просека даје се тежина вредности да би се добио одређени одговор.
Просечна и пондерисана просечна разлика
Погледајмо сада међусобне разлике.
| Основа | Просек | Пондерисана | ||
| Дефиниција | То је збир свих појединачних запажања подељен бројем запажања. | То је посматрање помножено са тежином и сабрано да би се пронашло решење. | ||
| Једначина | То је математичка једначина. | Примењује се у свакодневним финансијским активностима. | ||
| Решење | То је приказ скупа података. | Треба да процени да би се дошло до решења проблема. | ||
| Калкулације | То се може решити за скуп података помоћу аритметичке формуле. | Компонента добија тежину вредности да би стигла до одређеног одговора. |
Закључак
Дакле, видели смо просек у односу на пондерисани просек и видели смо разлику између њих двоје. Видели смо да је просек збир свих појединачних посматрања подељен бројем посматрања, а просек се може решити за скуп података помоћу аритметичке формуле, док је пондерисани просек посматрање помножено са пондером и сабрано да би се пронашло раствору и пондерисаној просечној компоненти дата је тежина вредности да би се дошло до одређеног одговора. Обоје имају различите кориснике на основу проблема и обојица се рачунају различито. Главна сврха пондерисаног просека је да пронађе праву тежину или вредност за решавање. Пондерисани просек је просечна вредност отплате главнице одређених обвезница или зајмова све док се главница не плати. А просек се користи за проналажење средње вредности или просечне вредности.