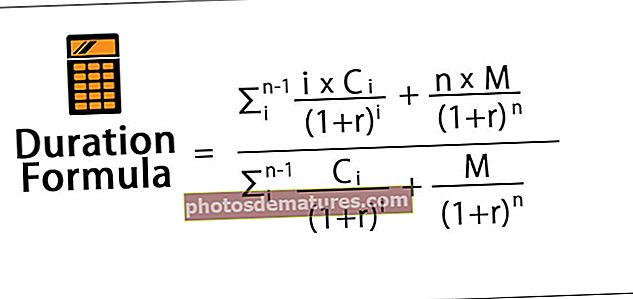photosdematures.com

Дефиниција Схарпе-овог односа

Шарпов однос је однос који је развио Виллиам Ф. Схарпе и користе га инвеститори како би извели вишак просечног приноса портфеља преко безризичне стопе приноса, по јединици волатилности (стандардне девијације) портфеља.

Објашњење

Схарпе Ратио је критична компонента за обележавање укупних приноса на портфељу. То је просечни приход који је остварен већи од безризичног приноса у поређењу са укупним износом ризика који се сноси. То је начин да се испитају перформансе инвестиције прилагођавањем њене компоненте ризика. Шарпов однос карактерише колико добро повраћај имовине компензује инвеститора за преузет ризик. Када се упоређују две активе у односу на заједничку меру, она са вишим Схарпе-овим односом је назначена као повољна прилика за инвестирање при истом нивоу ризика.

Ако погледате горњу табелу, видећете да ПРВЦКС има већи Схарпе Ратио од 1,48 и да је најбољи фонд у својој групи.

Шарпов однос, као и било који други математички модел, ослања се на тачност података који морају бити тачни. Док се испитују инвестиционе перформансе имовине са углађивањем приноса, Схарпеов однос би се изводио из перформанси основне имовине, а не из приноса фонда. Овај однос, заједно са Треинор Ратиос и Јесон'с Алпхас, често се користи за рангирање учинка различитих портфеља или менаџера фондова.

Формула

1966. године Виллиам Схарпе је развио овај однос који се првобитно називао односом „награде и променљивости“ пре него што су га наредни академици и финансијски оператери почели називати Схарпе-овим односом. Дефинисано је на више начина док на крају није уцртано као доле:

Формула Схарпе-овог односа = (Очекивани повратак - Ризична стопа поврата) / Стандардна девијација (променљивост)

Неки од појмова које морамо разумети су:

• Повратак - Поврати могу бити различитих фреквенција, попут дневних, недељних, месечних или годишњих, све док је дистрибуција нормално расподељена, јер се ти приноси могу годишње израчунати како би се постигли прецизни резултати. Ненормалне ситуације попут виших врхова, искривљености дистрибуције могу бити проблематично подручје за однос јер стандардна девијација нема исту ефикасност када постоје ови проблеми.
• Стопа поврата без ризика - Ово се користи за процену да ли се неко правилно надокнађује за додатни ризик који сноси због ризичне имовине. Традиционално, стопа приноса без финансијског губитка су државне хартије од вредности са најкраћим трајањем (нпр. Амерички трезорски записи). Иако таква варијанта осигурања има најмању количину волатилности, може се тврдити да би се такве хартије од вредности требале подударати са другим хартијама од вредности истог трајања.
• Стандардна девијација - То је величина која изражава колико се јединица из датог скупа променљивих разликује од Средњег просека групе. Једном када се израчуна овај вишак приноса у односу на принос без ризика, мора се поделити са стандардном девијацијом ризичног средства које се мери. Што је већи број, привлачна ће се инвестиција појавити из перспективе ризика / поврата. Међутим, уколико стандардна девијација није суштински велика, компонента полуге можда неће утицати на однос. И бројник (повратак) и називник (стандардна девијација) могу се удвостручити без проблема.

Пример

Клијент „А“ тренутно држи 450 000 УСД уложених у портфељ са очекиваним приносом од 12% и променљивошћу од 10%. Ефикасан портфељ има очекивани принос од 17% и колебљивост од 12%. Безризична каматна стопа износи 5%. Шта је однос Шарпа?

Формула Схарпе-овог односа = (Очекивани повратак - Ризична стопа поврата) / Стандардна девијација (променљивост)

Шарпов однос = (0,12-0,05) /0,10 = 70% или 0,7к

Израчунавање Схарпе-овог односа у програму Екцел

Сад кад знамо како формула функционише, израчунајмо Схарпе Ратио у екцелу.

Корак 1 - Добијте поврат у табеларном формату

Први корак укључује организовање поврата портфеља узајамног фонда који желите да анализирате. Период може бити месечни, квартални или годишњи. Табела у наставку даје годишње приносе узајамног фонда.

Корак 2 - Добијте детаље поврата без ризика у табели

У овој доњој табели претпоставио сам да безризични повратак износи 3,0% током периода од 15 година. Међутим, стопа без ризика може се мењати сваке године и тај број морате да ставите овде.

Корак 3 - Пронађите повраћај вишка

Трећи корак у израчунавању Схарпе-овог односа у екцелу је проналажење вишка приноса портфеља. У нашем случају, вишак поврата је Годишњи повратак - Поврат без ризика.

Корак 4 - Пронађите просек годишњег поврата.

Четврти корак у израчунавању Схарпе-овог односа у екцелу је проналажење просека годишњих приноса. Можете користити Екцел формулу ПРОСЕКО да бисте пронашли просек портфеља. У нашем примеру добијамо просечан принос од 12,09%.

Корак 5 - Пронађите стандардно одступање од вишка повраћаја

Да бисте пронашли стандардно одступање вишка приноса, можете користити екцел формулу СТДЕВ како је дато у наставку.

Корак 6 - Израчунајте однос Шарпа

Последњи корак за израчунавање Схарпе-овог односа у екцелу је подела просечних приноса стандардном девијацијом. Добијамо однос = 12,09% / 8,8% = 1,37к

Добијамо однос = 12,09% / 8,8% = 1,37к

Предности коришћења Схарпе Ратио-а

# 1 - Схарпе Ратио помаже у поређењу и упоређивању додавања нових средстава

Користи се за упоређивање варијансе укупних карактеристика поврата ризика поврата портфеља кад год му се дода ново средство или класа имовине.

• На пример, портфолио менаџер разматра додавање алокације робног фонда свом постојећем инвестиционом портфељу 80/20 акција са Схарпе-овим односом од 0,81.
• Ако је издвајање новог портфеља 40/40/20 акција, обвезница и издвајања дужничког фонда, Схарпе-ов однос се повећава на 0,92.

Ово је показатељ да, иако је улагање у робни фонд нестабилно као самостална изложеност, у овом случају то заправо доводи до побољшања карактеристике поврата ризика у комбинованом портфељу, а самим тим додаје предност диверзификације у другу имовину класе постојећем портфељу. Мора бити укључена пажљива анализа да би додељивање средстава могло касније да се промени ако то има негативан ефекат на здравље портфеља. Ако додавање нове инвестиције доводи до смањења односа, не би требало да буде укључено у портфељ.

# 2 - Шарпов однос помаже у поређењу поврата ризика

Овај однос такође може да пружи смернице о томе да ли су прекомерни приноси портфеља резултат пажљивог доношења инвестиционих одлука или су резултат непримерених ризика. Иако појединачни фонд или портфељ могу имати веће приносе од својих вршњака, разумно је улагање само ако ти већи приноси не дођу са непримереним ризицима. Што је већи Схарпеов однос портфеља, то су његове перформансе боље утицале на компоненту ризика. Негативни Шарпов однос указује на то да би мање ризична имовина имала боље резултате од хартије од вредности која се анализира.

Узмимо пример поређења ризик-повратак.

Претпоставимо да је портфолио А имао или се очекује да има стопу приноса од 12% са стандардном девијацијом од 0,15. Под претпоставком референтног приноса од око 1,5%, стопа поврата (Р) била би 0,12, Рф би била 0,015, а ’с’ би било 0,15. Однос ће се читати као (0,12 - 0,015) / 0,15 што израчунава 0,70. Међутим, овај број ће имати смисла када се упореди са другим портфељем, рецимо Портфолио ‘Б’

Ако портфељ „Б“ показује већу варијабилност од портфеља „А“, али има исти принос, имаће већу стандардну девијацију са истом стопом поврата из портфеља. Под претпоставком да је стандардна девијација за портфељ Б 0,20, једначина би се читала као (0,12 - 0,015) / 0,15. Шарпов однос овог портфеља биће 0,53, што је ниже у поређењу са портфељем „А“. Ово можда није запањујући резултат, узимајући у обзир чињеницу да обе инвестиције нуде исти повраћај, али „Б“ има већи квантум ризика. Очигледно је да ће она која има мање ризика понудити исти поврат бити преферирана опција.

Критике о односу Шарпа

Шарпов однос користи Стандардну девијацију приноса у називнику као алтернативу укупним ризицима портфеља, уз претпоставку да су приноси равномерно распоређени. Претходно тестирање показало је да приноси одређених финансијских средстава могу одступати од нормалне расподеле, што резултира релевантним тумачењима Схарпе-овог односа као погрешним.

Овај однос могу побољшати разни менаџери фондова који покушавају да повећају свој очигледни принос прилагођен ризику, који се може извршити на следећи начин:

1. Повећавање временског трајања које се мери: Ово ће резултирати мањом вероватноћом волатилности. На пример, годишња стандардна девијација дневних приноса је углавном већа од недељних, што је заузврат веће од оне месечних. Што је временско трајање веће, јаснија слика мора да искључи неке појединачне факторе који могу утицати на укупне перформансе.
2. Састављање месечних приноса али рачунање стандардне девијације искључујући овај недавно израчунати сложени месечни повратак.
3. Писање одлука о продаји и куповини портфеља без новца: Таква стратегија може потенцијално повећати приносе прикупљањем премије за опције без исплате током низа година. Стратегије које укључују изазивање ризика неплаћања, ризика ликвидности или других облика широко распрострањених ризика поседују исту способност извештавања о непристрасном Схарпе-овом односу.
4. Углађивање поврата: Коришћење одређених изведених структура, нерегуларно обележавање на тржишту мање ликвидних средстава или коришћење одређених модела цена који подцењују месечну добит или губитак, могу смањити очекивану колебљивост.
5. Елиминисање екстремних повратака: Превисоки или прениски приноси могу повећати пријављену стандардну девијацију било ког портфеља јер је то удаљеност од просека. У таквом случају, менаџер фонда може одлучити да елиминише крајње месечне приносе (најбоље и најгоре) месечно сваке године како би смањио стандардно одступање и утицао на резултате, јер таква једнократна ситуација може утицати на укупан просек.

Однос ек-Анте и ек-пост Схарпе-а

Шарпов однос је ревидиран више пута, али два општа облика која су коришћена су ек-анте (предвиђање будућег приноса и варијансе) и ек-пост (анализа претходне варијанце повратка).

• Ек-анте однос Шарпа предвиђања су једноставна за процените обрасце након запажања прошлих перформанси сличних инвестиционих активности.
• Ек-пост однос Шарпа мери колико су поврати били високи у односу на то колико су ти приноси били различити током датог временског периода. Прецизније, то је однос диференцијалних приноса (разлика између поврата улагања и референтне инвестиције) наспрам историјске променљивости (стандардне девијације) тих приноса.

Закључак

Шарпов однос је стандардно мерило перформанси портфеља. Због своје једноставности и лакоће тумачења, један је од најпопуларнијих индекса. Нажалост, већина корисника заборавља на претпоставке које резултирају непримереним исходом. Требали бисте размислити о провери расподеле приноса или валидацији резултата са еквивалентним мерама учинка пре него што донесете одлуку на тржишту.