photosdematures.com

Формула за израчунавање ученикове Т расподеле

Формула за израчунавање Т расподеле (која је у народу позната и као Студентова Т расподела) приказана је као Одузимање средње вредности популације (средња вредност другог узорка) од средње вредности узорка (средња вредност првог узорка) која је [к-бар - μ] која се затим дели стандардном девијацијом средњих вредности која се у почетку дели квадратним кореном од н који је број јединица у том узорку [с ÷ √ (н)].

Расподела Т је врста дистрибуције која изгледа готово као нормална крива дистрибуције или крива звона, али са нешто дебљим и краћим репом. Када је величина узорка мала, тада ће се користити ова расподела уместо нормалне расподеле.

Где,

• к је средња вредност узорка
• μ је средња вредност популације
• с је стандардна девијација
• н је величина датог узорка

Прорачун дистрибуције Т.

Израчун студентске т расподеле је прилично једноставан, али да, вредности су потребне. На пример, треба имати средњу вредност популације, а то је универзум, што није ништа друго до просек популације, док је средња вредност узорка потребна да би се проверила аутентичност популације, да ли је изјава која се тврди на основу популације заиста тачна и да ли је узета представљаће исту изјаву. Дакле, формула расподеле т овде одузима средњу вредност узорка од средње вредности популације, а затим је дели стандардном девијацијом и вишеструком квадратном корену величине узорка да би се стандардизовала вредност.

Међутим, с обзиром да не постоји опсег за израчунавање т дистрибуције, вредност може ићи чудно и нећемо моћи да израчунамо вероватноћу јер ученикова т дистрибуција има ограничења у постизању вредности, па је стога корисна само за мању величину узорка. Такође за израчунавање вероватноће након постизања резултата потребно је пронаћи вредност тога из ученикове т табеле расподеле.

Примери

Овде можете преузети овај Т Дистрибутивни Екцел образац - Т Дистрибутион Екцел Темплате

Пример # 1

Узмите у обзир следеће променљиве које су вам дате:

• Просек становништва = 310
• Стандардна девијација = 50
• Величина узорка = 16
• Средња вредност узорка = 290

Израчунати вредност т-расподеле.

Решење:

За израчунавање дистрибуције Т. користите следеће податке.

Дакле, прорачун дистрибуције Т може се извршити на следећи начин -

Овде су дате све вредности, само их треба уградити.

Можемо користити формулу расподеле т

Вредност т = (290 - 310) / (50 / √16)

Т вредност = -1,60

Пример # 2

Компанија СРХ тврди да њени запослени на нивоу аналитичара зарађују у просеку 500 долара на сат. Одабран је узорак од 30 запослених на нивоу аналитичара, а просечна зарада по сату износила је 450 УСД са одступањем узорка од 30 УСД и претпостављајући да је њихова тврдња тачна, израчунајте вредност т-дистрибуције која ће се користити за проналажење вероватноће за т - дистрибуција.

Решење:

За израчунавање дистрибуције Т. користите следеће податке.

Дакле, прорачун дистрибуције Т може се извршити на следећи начин -

Овде су дате све вредности, само их треба уградити.

Можемо користити формулу расподеле т

Вредност т = (450 - 500) / (30 / √30)

Т вредност = -9,13

Отуда је вредност за т резултат -9,13

Пример # 3

Универзални одбор колеџа применио је тест нивоа ИК за 50 насумично изабраних професора. А резултат који су из тога пронашли био је просечни резултат ИК-а 120 са варијанцом 121. Претпоставимо да је т-резултат 2.407. Шта значи популација за овај тест који би оправдао вредност т резултата као 2.407?

Решење:

За израчунавање дистрибуције Т. користите следеће податке.

Овде су све вредности дате заједно са вредношћу т, овог пута треба израчунати средњу вредност становништва уместо вредности т.

Опет, користили бисмо расположиве податке и израчунали ћемо средства популације уметањем вредности даних у доњој формули.

Средња вредност узорка је 120, средња популација је непозната, стандардна девијација узорка биће квадратни корен варијансе који би био 11, а величина узорка је 50.

Дакле, израчунавање средње вредности популације (μ) може се извршити на следећи начин -

Можемо користити формулу расподеле т

Вредност т = (120 - μ) / (11 / √50)

2.407 = (120 - μ) / (11 / √50)

-μ = -2,407 * (11 / √50) -120

Средња популација (μ) биће -

μ = 116,26

Отуда ће вредност за популацијску средину бити 116,26

Релевантност и употреба

Расподела Т (и оне придружене вредности резултата т) користе се у тестирању хипотеза када треба сазнати да ли треба одбити или прихватити нулту хипотезу.

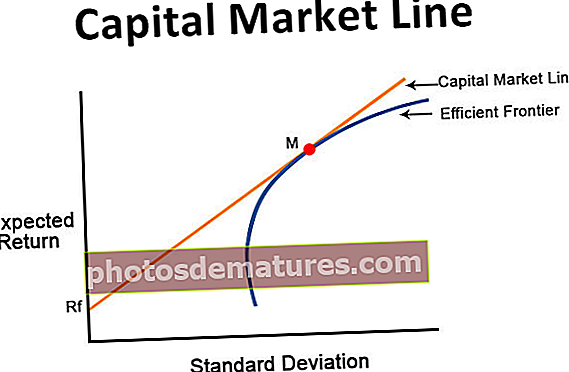
На горњем графикону, централни регион ће бити подручје прихватања, а репни регион ће бити одбијање. На овом графикону, који је двострани тест, плаво осенчено ће бити подручје одбијања. Подручје у пределу репа може се описати или т-резултатима или з-резултатима. Узмимо пример, слика лево ће приказати површину у реповима од пет процената (што је 2,5% са обе стране). З-резултат треба да буде 1,96 (узимајући вредност из з-табеле), што ће представљати оних 1,96 стандардних одступања од просека или средње вредности. Нулта хипотеза се може одбити ако је вредност з оцене мања од вредности -1,96 или је вредност з оцене већа од 1,96.

Генерално, ова расподела ће се користити као што је раније описано када неко има мању величину узорка (углавном испод 30) или ако не зна колика је варијанса популације или стандардна девијација популације. Из практичних сврха (то је у стварном свету), то би углавном било увек случај. Ако је величина узорка који је дат довољно велика, тада ће 2 расподеле бити практично сличне.