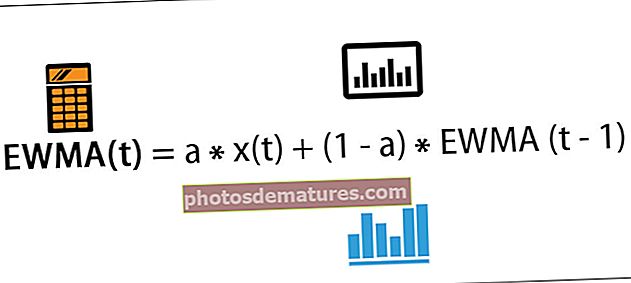photosdematures.com

Колика је будућа вредност ренте?

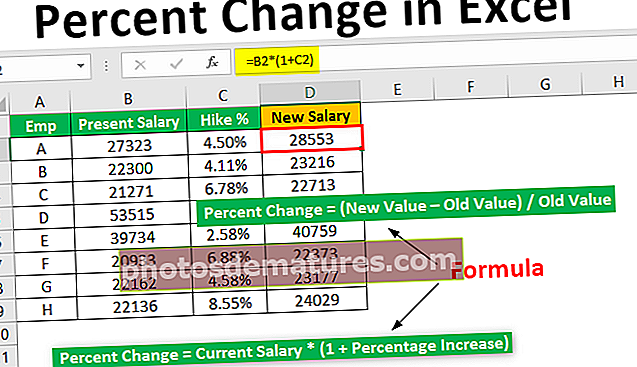
Будућа вредност доспелог ануитета је вредност износа који ће се примити у будућности, где се свака уплата врши на почетку сваког периода, а формула за њен израчун је износ сваке ануитетне помножене каматне стопе у број периода минус један који се дели каматном стопом и целина се множи са једном плус каматном стопом.

Будућа вредност формуле доспећа ануитета

Математички је представљен као,

ФВА _Због = П * [(1 + р) н - 1] * (1 + р) / р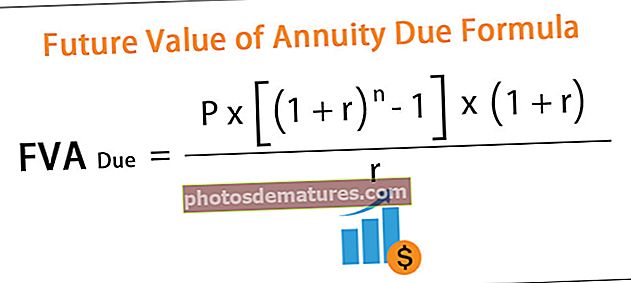

где је ФВА _Због = Будућа вредност доспелог ануитета

• П = Периодично плаћање
• н = Број периода
• р = ефективна каматна стопа

Како израчунати? (Корак по корак)

• Корак 1: Прво, схватите исплате које ће се платити у сваком периоду. Имајте на уму да је горња формула применљива само у случају једнаких периодичних плаћања. Означава се са П.
• Корак 2: Даље, схватите каматну стопу која се наплаћује на основу преовлађујуће тржишне стопе. То је каматна стопа коју инвеститор прима ако новац улаже на тржиште. Да бисте добили ефективну каматну стопу, поделите годишњу каматну стопу са бројем периодичних плаћања у години. Означава се са р. тј р = Годишња каматна стопа / Број периодичних плаћања у години
• Корак 3: Даље, укупан број периода израчунава се множењем броја периодичних уплата у години и броја година. Означава се са н. тј н = Број година * Број периодичних уплата у години
• Корак 4: Коначно, будућа вредност доспелог ануитета израчунава се на основу периодичног плаћања (корак 1), ефективне каматне стопе (корак 2) и броја периода (корак 3) као што је горе приказано.

Примери

Ову будућу вредност предлошка за исплату ренте можете преузети овде - Будућа вредност предлошка за исплату ренте у Екцел-у

Пример # 1

Узмимо пример Џона Доа који планира да положи 5.000 долара на почетку сваке године у наредних седам година како би уштедео довољно новца за образовање своје ћерке. Утврдите износ који ће Јохн Дое имати на крају седам година. Имајте на уму да је тренутна каматна стопа на тржишту 5%.

Израчунајте ФВ ренте која доспева за периодично плаћање користећи горе дате информације,

ФВ ренте_Због = П * [(1 + р) н - 1] * (1 + р) / р

= $5,000 * [(1 + 5%)7 – 1] * (1 + 5%) / 5%

Будућа вредност доспећа ануитета биће -

= $42,745.54 ~ $42,746

Према томе, после седам година Јохн Дое ће морати да потроши 42.746 долара за образовање своје ћерке.

Пример # 2

Узмимо још један пример Никсонових планова да акумулира довољно новца за свој МБА. Одлучује да уплати месечну уплату од 2.000 УСД за наредне четири године (почетком сваког месеца), тако да може да прикупи потребну количину новца. Према саветнику за образовање, Никон ће захтевати 100.000 УСД за свој МБА. Проверите да ли ће Никонови депозити финансирати његове планове за МБА с обзиром на то да је тренутна каматна стопа коју банка наплаћује 5%.

Дато,

• Месечна уплата, П = 2.000 УСД
• Ефективна каматна стопа, р = 5% / 12 = 0,42%
• Број периода, н = 4 * 12 месеци = 48 месеци

Израчунајте ФВ доспећа ренте за месечно плаћање користећи горе дате информације,

= $2,000 * [(1 + 0.42%)48 – 1] * (1 + 0.42%) / 0.42%

Будућа вредност месечне исплате биће -

ФВ ренте_Због = $106,471.56 ~ $106,472

Дакле, са планираним депозитима, очекује се да Никон има 106 472 УСД, што је више од износа (100 000 УСД) потребног за његов МБА.

Релевантност и употреба

Будућа вредност доспелог ануитета је још један израз ТВМ-а, данас примљени новац може се уложити сада и растаће током одређеног временског периода. Једна од његових упечатљивих примена је у израчунавању премија за полисе животног осигурања. Такође проналази примену у обрачуну резервног фонда где месечни допринос од зараде делује као периодична уплата. Будућа вредност ануитета расте на основу наведене дисконтне стопе, јер ће таква већа дисконтна стопа бити већа и будућа вредност ануитета.