photosdematures.com

Шта је мултиколинеарност?

Мултиколинеарност је статистички феномен у којем су две или више променљивих у регресионом моделу зависне од осталих променљивих на такав начин да се једна може линеарно предвидети од друге са високим степеном тачности. Генерално се користи у опсервационим студијама и мање је популаран у експерименталним студијама.

Врсте мултиколинеарности

Постоје четири врсте мултиколинеарности

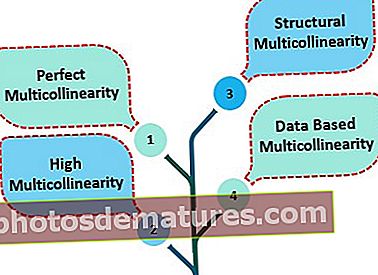
• #1 –Савршена мултиколинеарност - Постоји када независне променљиве у једначини предвиђају савршену линеарну везу.
• # 2 - Висока мултиколинеарност - Односи се на линеарни однос између две или више независних променљивих које нису у међусобној корелацији.
• # 3 - Структурна мултиколинеарност - То узрокује сам истраживач уметањем различитих независних променљивих у једначину.
• # 4 - Мултицоллинеаарност заснована на подацима - Узроковано је експериментима које је истраживач лоше дизајнирао.

Узроци мултиколинеарности

Независне променљиве, промена параметара променљивих чини да мала промена променљивих има значајан утицај на резултат и прикупљање података односи се на узорак одабране популације која се узима.

Примери мултиколинеарности

Пример # 1

Претпоставимо да је АБЦ Лтд КПО ангажована од фармацеутске компаније да пружа услуге истраживања и статистичку анализу болести у Индији. За ово је АБЦ доо изабрао доб, тежину, професију, висину и здравље као примарне параметре.

• У горњем примеру постоји ситуација мултиколинеарности јер су независне променљиве одабране за студију директно повезане са резултатима. стога би било упутно да истраживач прво прилагоди променљиве пре започињања било ког пројекта, јер ће на резултате овде директно утицати одабране променљиве.

Пример # 2

Претпоставимо да је компанију Тата Моторс именовало АБЦ Лтд да би се схватило да ће обим продаје тата мотора бити висок у којој категорији на тржишту.

• У горњем примеру, прво ће се финализовати независне променљиве на основу којих истраживање треба да буде завршено. то може бити месечни приход, старост. марка, нижа класа. Значи само да ће бити изабрани подаци који ће се уклопити у све ове картице како би се схватило колико људи може купити овај аутомобил (тата нано), а да ни један други аутомобил не погледа.

Пример # 3

Претпоставимо да је ангажована компанија АБЦ Лтд да поднесе извештај да би знала колико је људи млађих од 50 година склоно срчаном удару. за ово су параметри старост, пол, историја болести

• У горњем примеру постоји мултиколинеарност која је настала зато што независну променљиву „старост“ треба подесити на старост млађу од 50 година за позивање јавних пријава како би се особе старије од 50 година аутоматски филтрирале.

Предности

Испод су неке од предности

• Линеарни однос између независних променљивих у једначини.
• Веома корисно у статистичким моделима и истраживачким извештајима које су припремиле компаније засноване на истраживању.
• Директан утицај на жељени резултат.

Мане

Испод су неки од недостатака

• У неким ситуацијама овај проблем би се решио прикупљањем више података о променљивим.
• Нетачна употреба думми променљивих, тј. Истраживач може заборавити да користи думми променљиве кад год је то потребно.
• Уметање 2 исте или идентичне променљиве у једначину попут кг и лбс у пондерима.
• Уметање променљиве у једначину која је комбинација 2.
• Компликовано за извођење прорачуна јер је то статистичка техника и захтева извршење статистичких калкулатора.

Закључак

Мултиколинеарност је један од најпожељнијих статистичких алата који се често користи у регресионој анализи и статистичкој анализи великих база података и жељеног резултата. Све велике компаније у својој компанији имају одвојено статистичко одељење које врши статистичку регресиону анализу о производима или људима како би менаџменту пружио стратешки поглед на тржиште и такође им помогао да направе своје дугорочне стратегије водећи рачуна о томе. Графички приказ анализе даје читаоцу јасну слику о директном односу, тачности и учинку.

• Ако је циљ истраживача да разуме независне променљиве у једначини, онда ће му мултиколинеарност представљати велики проблем.
• Истраживач треба да изврши потребне промене у променљивим у самој фази 0, иначе може имати огроман утицај на резултате.
• Мултиколинеарност се може постићи испитивањем матрице корелације.
• Санационе мере играју значајну улогу у решавању проблема мултиколинеарности.