photosdematures.com

МИНВЕРСЕ функција у програму Екцел

МИНВЕРСЕ у Екцелу означава „Матрик Инверсе“. Ова уграђена Екцел функција претвара дату матрицу у инверзну матрицу са истим бројем низова.

Разговарајући о „инверзној матрици“ треба схватити о чему се тачно ради у „инверзној матрици“.

Инверзна матрица: Реципрочна вредност броја назива се „инверзна матрица“. На пример, за број 5 можемо реципрочно написати као

Дакле, инверзна матрица се може написати у истој логици помоћу ове једначине „А-1“ а горњи број се може записати као 5-1 такође. Када помножимо број са његовим реципрочним знаком, увек добијемо 1 као последица. На пример, број 5 се помножи са његових реципрочних 1/5, а резултат добијамо као 13

Слично томе, када помножимо матрицу са њеном инверзном, добијамо матрицу идентитета, тј. „Ја“. Испод је једначина матрице идентитета.

А * А-1 = И.

Када говоримо о инверзној матрици у екцелу, морамо да погледамо и матрицу идентитета. Са идентификационом матрицом сав број редова и колона је у једнаком броју, са дијагоналом добијамо 1 као вредност, а осим дијагонале, све остало ће бити једнако нули.

Дакле, идентитетска матрица ће увек бити у облику “2 * 2, 3 * 3, 4 * 4” овако.

Једном када је матрица обрнута, можемо унакрсно провјерити да ли је обрнута или не користећи функцију ММУЛТ у екцелу и добићемо матрицу идентитета која изгледа овако.

Ок, пробајмо сада ове ствари са екцелом.

Пример употребе МИНВЕРСЕ Екцел функције

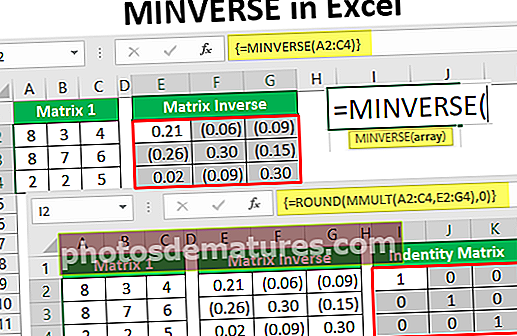
Ову МИНВЕРСЕ у Екцел предлошку можете преузети овде - МИНВЕРСЕ у Екцел предлошку

На пример, погледајте доњу матрицу 3 * 3.

• Имамо матричне бројеве од А2 до Ц4, да бисмо обрнули ову матрицу створили идентичну табелу поред горње табеле, али не задржавамо исте вредности и држимо поље празно.

• У опсегу Е2 до Г4 креираћемо инверзу матрице. Изаберите опсег ћелија од Е2 до Г4.

• Сада у одабраном опсегу ћелија отворите екцел МИНВЕРСЕ функцију.

• Први аргумент функције МИНВЕРСЕ је низ тј. ово није ништа друго до опсег вредности матрице који покушавамо да обрнемо, па су наше вредности матрице 3 * 3 у опсегу од А2 до Ц4.

Пре него што затворимо формулу, морамо имати на уму да је „МИНВЕРСЕ“ низ, тако да формулу морамо затворити помоћу тастера „ЦСЕ“.

Белешка: ЦСЕ је кратица за „Цтрл + Схифт + Ентер“. Дакле, све формуле низа затворене су само овим кључевима.

• Затворите формулу тако што ћете притиснути тастер ЕНТЕР држећи заједно тастер „Цтрл + Схифт“.

Као што видите горе, добили смо „инверзну матрицу“ помоћу функције МИНВЕРСЕ. Будући да је реч о формули низа, можемо видети коврџаве заграде ({}) на почетку и на крају формуле низа.

Сада можемо унакрсно провјерити да ли је ова матрица инверзна или не користећи функцију ММУЛТ. Функција ММУЛТ означава „Матрик Мултиплицатион“.

• Сада изаберите опсег ћелија да бисте креирали другу матрицу идентитета, па одаберите подручје матрице 3 * 3.

• Сада отворите функцију ММУЛТ за изабрани опсег ћелија.

• За низ1 аргумент функције ММУЛТ одаберите опцију „Матрица 1“ од А2 до Ц4.

• За арраи2 аргумент функције ММУЛТ одаберите опсег ћелија од „Е2 до Г4“ „Инверзна матрица“.

• ММУЛТ је такође функција низа, зато затворите формулу помоћу тастера „ЦСЕ“ за претварање у функцију низа.

• Овај резултат нам је дао децималне резултате, па користите функцију РОУНД унутар функције низа да бисте добили тачну „матрицу идентитета“.

Сада смо добили „матрицу идентитета“ где имамо 1 као дијагоналну вредност. Овако, помоћу функције МИНВЕРСЕ можемо обрнути матрицу и ММУЛТ да проверимо да ли је обрнута или не.

Ствари које треба запамтити

• Функција МИНВЕРСЕ може истовремено прихватити само једну матрицу.
• Ово је функција низа у Екцелу, па користите тастере „ЦСЕ“ да бисте затворили формулу.
• Када је матрица инверзна, идентитетску матрицу можемо пронаћи користећи функцију ММУЛТ где треба да помножимо оригиналну матрицу са инверзном матрицом.