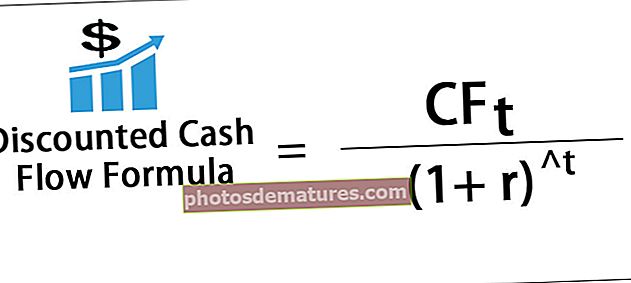photosdematures.com

Дефиниција ефективне каматне стопе

Ефективна каматна стопа, такође позната као годишња еквивалентна стопа, је каматна стопа коју лице стварно плати или заради на финансијски инструмент која се израчунава узимајући у обзир ефекат сложења током одређеног временског периода.

Формула ефективне каматне стопе

Формула ефективне каматне стопе = (1 + и / н) н -

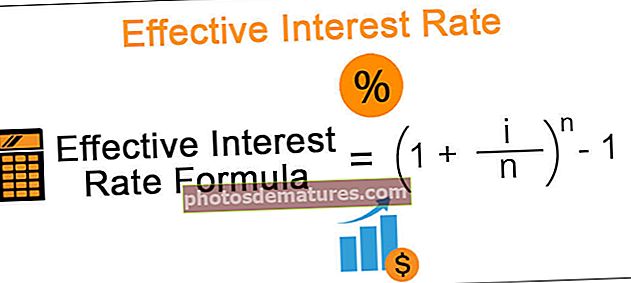
Овде је и = годишња каматна стопа која је наведена у инструменту.

н = Представља број периода сложења у години.

Тумачења

Компликовање мења каматну стопу. Због тога камата написана на инструмент није ефективна каматна стопа (годишња еквивалентна стопа) за инвеститора. На пример, ако је на инструменту написана каматна стопа од 11%, а каматна стопа се компликује четири пута годишње, тада годишња еквивалентна стопа не може бити 11%.

Шта би то онда било?

Било би - (1 + и / н) н - 1 = (1 + 0,11 / 4) 4 - 1 = 1,1123 - 1 = 0,1123 = 11,23%.

То значи да би 11,23% била ефективна каматна стопа за инвеститора.

Чак и ако је промена оскудна, није иста као годишња каматна стопа наведена у инструменту.

Пример

Пример # 1

Тинг је купио одређени инструмент. Каматна стопа наведена на инструмент је 16%. Уложио је око 100.000 америчких долара. Инструмент се меша годишње. Која би била ефективна каматна стопа (АЕР) за овај одређени инструмент? Колико би сваке године добио као камату?

Ефективна каматна стопа и годишња стопа нису увек исте, јер се камата сложи више пута годишње. Понекад се камата компликује полугодишње, квартално или месечно. И по томе се годишња еквивалентна стопа разликује од годишње каматне стопе.

Ово вам показује овај пример.

Израчунајмо.

Будући да се каматна стопа годишње компликује, ево формуле ефективне каматне стопе -

(1 + и / н) н - 1 = (1 + 0,16 / 1) 1 - 1 = 1,16 - 1 = 0,16 = 16%.

То значи да у овом конкретном примеру не би постојала разлика између годишње каматне стопе и годишње еквивалентне стопе (АЕР).

Сваке године Тинг би добио камату од = (100.000 УСД * 16%) = 16.000 УСД на инструмент.

Пример # 2

Тонг је купио одређени инструмент. Каматна стопа наведена на инструмент је 16%. Уложио је око 100.000 америчких долара. Инструмент се меша шест пута годишње. Која би била годишња еквивалентна стопа (АЕР) за овај одређени инструмент? Колико би сваке године добио као камату?

Ово је само продужетак претходног примера.

Али постоји огромна разлика.

У претходном примеру, инструмент се комбиновао једном годишње, што је годишњу каматну стопу учинило сличном годишњој еквивалентној стопи.

Међутим, у овом случају је сценарио потпуно другачији.

Овде имамо каматну стопу која се увећава шест пута годишње.

Дакле, ево формуле годишње каматне стопе -

(1 + и / н) н - 1 = (1 + 0,16 / 6) 6 - 1 = 1,171 - 1 = 0,171 = 17,1%.

Сада можете видети да ако се каматна стопа сложи шест пута годишње, годишња еквивалентна стопа постаје сасвим другачија.

Сада, пошто имамо ефективну каматну стопу, можемо израчунати камату коју ће Тонг добити на крају године.

Тонг ће добити = (100.000 УСД * 17.1%) = 17.100 УСД.

Ако упоредимо камате које Тинг добије у претходном примеру са Тонг-има јер се каматне стопе другачије састоје, видећемо да постоји око 1100 долара разлике у каматама.

Пример # 3

Пинг је инвестирао у инструмент. Уложила је 10.000 долара. Каматна стопа наведена у инструменту износи 18%. Камате се месечно увећавају. Откријте како ће Пинг примати камате сваког месеца.

Ово је много детаљан пример годишње еквивалентне стопе.

У овом примеру ћемо показати како се обрачун заправо дешава без употребе формуле ефективне каматне стопе.

Хајде да погледамо.

С обзиром да се каматна стопа месечно компликује, стварни распад поменуте каматне стопе месечно је = (18/12) = 1,5%.

• Првих месец дана Пинг ће добити камату од = (10 000 * 1,5%) = 150 УСД.
• У другом месецу, Пинг ће добити камату од = {(10,000 + 150) * 1,5%} = (10,150 * 1,5%) = 152,25 УСД.
• У трећем месецу, Пинг ће добити камату од = {(10.000 + 150 + 152,25) * 1,5%} = (10.302,25 * 1,5%) = 154,53 УСД.
• У четвртом месецу, Пинг ће добити камату од = {(10.000 + 150 + 152.25 + 154.53) * 1.5%} = (10.456,78 * 1.5%) = 156.85 УСД.
• У петом месецу, Пинг ће добити камату од = {(10.000 + 150 + 152.25 + 154.53 + 156.85) * 1.5%} = (10.613,63 * 1.5%) = 159,20 УСД.
• У шестом месецу, Пинг ће добити камату од = {(10.000 + 150 + 152.25 + 154.53 + 156.85 + 159.20) * 1.5%} = (10.772,83 * 1,5%) = 161,59 УСД.
• У седмом месецу, Пинг ће добити камату од = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59) * 1,5%} = (10 934,42 * 1,5%) = 164,02 УСД.
• У осмом месецу, Пинг ће добити камату од = {(10.000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02) * 1.5%} = (11098.44 * 1.5%) = 166.48 УСД.
• У деветом месецу Пинг ће добити камату од = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48) * 1,5%} = (11264,92 * 1,5%) = 168,97 УСД.
• У десетом месецу Пинг ће добити камату од = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97) * 1,5%} = (11433,89 * 1,5%) = 171,51 УСД.
• У једанаестом месецу Пинг ће добити камату од = {(10,000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51) * 1,5%} = (11605,40 * 1,5%) = 174,09 УСД.
• У дванаестом месецу Пинг ће добити камату од = {(10.000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09) * 1.5%} = (11779.49 * 1.5%) = 176,69 долара.

Укупна камата коју је Пинг добио за годину је -

• (150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09 + 176.69) = $1956.18.

• Формула годишње еквивалентне стопе = (1 + и / н) н - 1 = (1 + 0,18 / 12) 12 - 1 = 1,195618 - 1 = 0,195618 = 19,5618%.

Дакле, камата коју би Пинг добио = (10.000 ^ ^ 19,5618%) = 1956,18 долара.

Ефективна каматна стопа у Екцелу

За проналажење ефективне каматне стопе или годишње еквивалентне стопе у екцелу користимо екцел функцију ЕФФЕЦТ.

• номинална_ стопа је каматна стопа
• нпер је број периода сложења у години

Погледајмо пример испод

• Ако имате номиналну каматну стопу од 10% сложену годишње, тада је годишња еквивалентна стопа иста као 10%.
• Ако имате номиналну каматну стопу од 10% сложену шестомесечно, тада је годишња еквивалентна стопа иста као 10,25%.
• Ако имате номиналну каматну стопу од 10% сложену квартално, тада је годишња еквивалентна стопа иста као 10,38%.
• Ако имате номиналну каматну стопу од 10% сложену месечно, тада је годишња еквивалентна стопа иста као 10,47%.
• Ако имате номиналну каматну стопу од 10% дневно, ефективна каматна стопа је иста као 10,52%.

Предложена читања

Ово је био водич за ефективну каматну стопу и њену дефиницију. Овде ћемо разговарати о формули ефективне каматне стопе заједно са детаљним прорачунима. За даља сазнања можете се позвати на следеће чланке

• Пример негативне каматне стопе
• Израчунајте стопу учешћа
• Разлике - дисконтна стопа у односу на каматну стопу
• Формула номиналне каматне стопе
• Коинтеграција
<