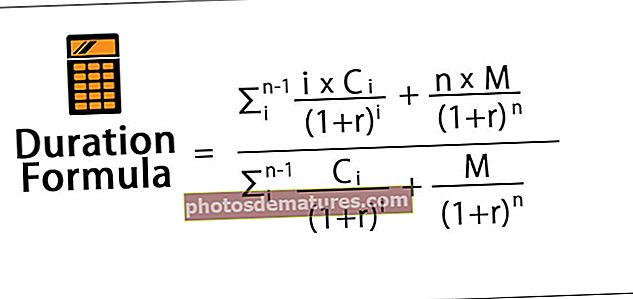photosdematures.com

Сложено интересовање за Екцел формулу

Заједнички интерес је додатак камате главници суме зајма или депозита, или можемо рећи камате на камате. Резултат је поновног улагања камате, уместо исплате, тако да се камате у наредном периоду зарађују на главници плус увећане претходно камате.

Док камата израчунава се само на главницу и (за разлику од сложених камата), а не на главницу увећану за камате зарађене или настале у претходном периоду (периодима).

Укупна акумулирана вредност, укључујући главницу П плус, сложену камату И, дата је формулом:

Где,

• П. је оригинална сума главнице
• П ’ је нова главница
• н је учесталост сложења
• р је номинална годишња каматна стопа
• т је укупна дужина времена примене камате (изражено коришћењем истих временских јединица као р, обично година).

Како израчунати сложену камату у Екцел формули? (са примерима)

Да схватимо исто користећи неке примере формуле сложене камате у екцелу.

Овај предложак сложене камате у Екцел-у можете преузети овде - предложак сложене камате у Екцелу

Пример # 1 - Коришћење Екцел формуле математичких сложених камата

Претпоставимо да имамо следеће информације за израчунавање сложене камате у екцелу.

Сада, пошто смо такође описали горњу формулу, применићемо исту у МС Екцел користећи референце ћелија у екцелу и разне операторе.

Корак 1 -Као Ц2 ћелија садржи главницу (можемо је назвати и садашњом вредношћу). Морамо да помножите ову вредност са каматном стопом.

Корак 2 -У нашем случају, интерес мора бити сложен тромесечно (Ц5) зато морамо годишњу каматну стопу поделити са ћелијом Ц5

Корак 3 -Како се камате састоје од четири пута годишње, треба да наведемо референцу ћелије у којој се помиње број година како бисмо могли помножити 4 са бројем година. Зато би формула била оваква:

Корак 4 -Након притиска на дугме Ентер, добићемо резултат као Рс. 15764.18 као будућу вредност са сложеним каматама.

Ово је сада као калкулатор сложених камата у Екцелу. Можемо променити вредност за годишњу каматну стопу, број година, и Сложени периоди годишње као испод.

Пример # 2 - Коришћење табеле за израчунавање сложених камата у екцелу

Претпоставимо да имамо следеће информације за израчунавање сложене камате у формату табеле екцел (систематски).

Корак 1 - Морамо назвати ћелију Е3 као ‘Оцени’ избором ћелије и променом имена помоћу Кутија са именом.

Корак 2 -Имамо главницу или садашњу вредност као 15000 а годишња каматна стопа је 5%. Да бисмо израчунали вредност инвестиције на крају 1. квартала, додаћемо 5% / 4, тј., 1,25% камате на главницу.

Резултат је приказан у наставку:

Корак 3 -Само треба да повучемо формулу до ћелије Ц6 избором опсега Ц3: Ц6и притиском Цтрл + Д..

Тхе будућност вредност након 4 четвртине биће Рс. 15764.18.

Пример # 3 - Сложена камата помоћу ФВСЦХЕДУЛЕ Екцел формуле

Претпоставимо да имамо следеће информације за израчунавање сложене камате у екцелу.

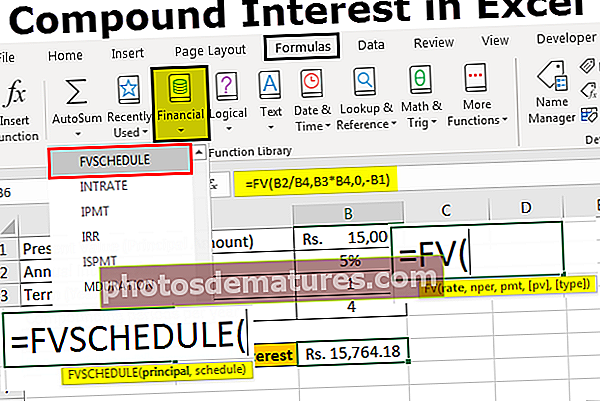
Користићемо ФВСЦХЕДУЛЕ функција за израчунавање будуће вредности. ФВСЦХЕДУЛЕ формула враћа будућу вредност почетне главнице након примене низа сложених каматних стопа.

Да бисте учинили исто, следећи кораци:

Корак 1 - Покренућемо писање функције ФВСЦХЕДУЛЕ у ћелију Б6. Функција узима два аргумента, тј. Главни и распоред.

• Заглавни, треба да дамо износ у који улажемо.
• Зараспоред, морамо да доставимо листу каматних стопа са зарезима у витичастим заградама да бисмо израчунали вредност са сложеном каматом.

Корак 2 - За „Главни“, пружићемо референцу Б1 ћелије и за ‘Распоред’, навешћемо 0,0125 јер је ово вредност коју добијамо када 5% поделимо са 4.

Резултат је приказан у наставку:

Сада примењујемо формулу ФВСЦХЕДУЛЕ у екцелу.

Корак 3 - Након притиска на дугме Ентер добијамо Рс. 15764.18 као будућу вредност са сложеном каматом у екцелу.

Пример # 4 - Сложена камата коришћењем формуле ФВ Екцел

Претпоставимо да имамо следеће податке за израчунавање сложене камате у екцелу.

Користићемо ФВ екцел формула за израчунавање сложених камата.

ФВ функција (означава Будућа вредност) враћа будућу вредност инвестиције на основу периодичних, сталних плаћања и константне каматне стопе.

Синтакса функције ФВ је

Аргумент у функцији ФВ је:

• Оцените: Стопа је стална каматна стопа по периоду у ануитету.
• Нпер: Нпер представља укупан број периода у ануитети.
• Пмт: ПМТ означава плаћање. Ово указује на износ који ћемо додавати ануитети сваког периода. Ако изоставимо да поменемо ову вредност, онда је обавезно споменути ПВ
• ПВ: ПВ представља садашњу вредност. Ово је износ у који улажемо. Како овај износ излази из нашег џепа, зато је по договору овај износ поменут са негативним предзнаком.
• Тип: Ово је опционални аргумент. Морамо да наведемо 0 ако се износ додаје инвестицији на крају периода или 1 ако се износ додаје инвестицији на почетку периода.

Морамо споменути или аргумент ПМТ или ПВ.

Навешћемо стопа као „Годишња каматна стопа (Б2) / сложени периоди годишње (Б4)“.

Морамо да прецизирамо нпер као „Термин (године) * Сложени периоди годишње“.

Како нећемо додавати никакав додатни износ главници између периода улагања, зато ћемо одредити „0“ за „Пмт“.

Као што смо изоставили вредност за „Пмт“ а ми улажемо Рс. 15000 као главницу (садашња вредност), даћемо референцу Б1 ћелије са негативним предзнаком за „ПВ“

Након притиска на тастер Ентер добијамо Рс. 15764.18 као будућу вредност са сложеним каматама.

Ствари које треба запамтити о формули сложене камате у програму Екцел

• Морамо да унесемо каматну стопу у процентном облику (4%) или у децималном облику (0,04).
• Као 'ПМТ ’ и „ПВ“ аргумент у ФВ функција је одлив у стварности, морамо их поменути у негативном облику (са знаком минус (-)).
• ФВ функција даје #ВАЛУЕ! Грешка када је било која нумеричка вредност дата као аргумент.
• Морамо напоменути било који ПМТ или ПВ аргумент у ФВ функција.