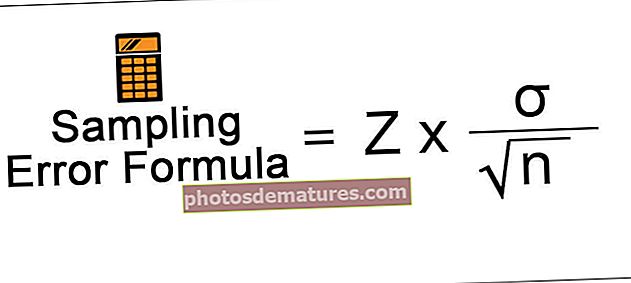photosdematures.com

Интерполација у Екцелу

Интерполација у екцелу помаже нам да пронађемо вредност између две тачке на линији графикона или линији криве. Једноставним речима „Интер“ предлаже да се погледа у податке које већ имамо. Не само у статистици, већ и на пољу науке, трговине, пословања користи се за проналажење или предвиђање будуће вредности која пада између две постојеће тачке података.

Пример интерполације података у Екцелу

Да бисмо разумели концепт интерполације података у Екцелу, погледајмо пример у наставку. У сеоској кући фармер узгаја необрађени рибе и непрестано прати раст необрађених риба.

Ову Интерполацију у Екцел предлошку можете преузети овде - Интерполација у Екцел предлошку

Фармер је забележио раст необрађених риба испод тренда за 20 дана, где је забележио раст једном у свака 4 дана.

Из горње табеле фармер жели да зна колико је необрађен био пети дан.

Увидом у податке можемо лако проценити да је пети дан падао на 2,5 инча. Разлог зашто лако можемо да утврдимо раст необрађеног усева, јер је нарастао линеарно, тј. Постојала је веза између броја забележених дана и пораста необрађеног пада. Испод је графикон који показује линеарни раст необрађених риба.

Горњи графикон лако приказује линеарни образац раста необрађених риба. Али ако је необрађена риба расла линеарно, тешко је предвидети раст од 5. дана.

На основу ове горње криве пољопривредници не могу да процене колики је био раст петог дана. Дакле, ту нам наш концепт интерполације помаже да пронађемо раст 5. дана.

За интерполацију имамо доњу формулу.

Овде имамо две променљиве, тј. Кс1 и И1. „Кс“ је први скуп вредности, а „И“ други скуп вредности.

У нашем примеру необрађеног раста први скуп вредности је (4,2). Овде је „4“ дан, а „2“ центиметар раста необрађених јастучића.

Други скуп вредности је (8,4). Овде је „8“ дан, а „4“ центиметри раста необрађених јастучића.

Будући да морамо да пронађемо раст променљиве „к“ за пети дан, постаје 5 у односу на променљиву инча раста „и“.

Дакле, применимо вредности на горњу формулу.

Сада направите прорачун првог корака.

Напомена „к“ је једнако

Дакле, пети дан раст необрађених јастука био би 2,5 инча.

Линеарна интерполација у Екцелу

Иста линеарна интерполација у екцелу води исте податке и у екцел.

Сада морамо да пронађемо центиметре раста за 5. дан, дакле к = 5.

Скуп 1 (к1, и1)

2. сет (к2, и2)

Тако к1 = 4, и1 = 2, к2 = 8 и и2 = 4.

Унесите ове вредности у Екцел ћелије листа.

Поменуо сам упитнике за к1, и1, к2 и и2. Јер помоћу ових једноставних података лако их можемо пронаћи само својим очима. Али увек је добра пракса проналажење ових вредности путем формуле. Да бисте пронашли вредност „к1“, примените доњу формулу.

Сада да бисте пронашли вредност „и1“, примените доњу формулу.

Да бисте пронашли вредност „к2“, примените доњу формулу.

Да бисте пронашли вредност „и2“, примените доњу формулу.

Овако користећи ове формуле, можемо пронаћи вредности за све параметре Интерполације у екцел формули.

Следеће да бисте пронашли центиметре за раст пешчаног дана, примените доњу формулу.

Дакле, како смо израчунали ручно помоћу формуле, добили смо и 2,5 као одговор. Ако је потребно, можемо уметнути линијски графикон за податке.

Ствари које треба овде запамтити

• Интерполација је поступак проналажења средње вредности постојећих података.
• У Екцелу не постоји уграђена формула за израчунавање вредности интерполације у Екцелу.
• У функцији МАТЦХ морамо да користимо „1“ за параметар „типе матцх“ који помаже корисницима да пронађу вредност већу од вредности претраживања.