photosdematures.com

Формула за израчунавање грешке узорковања

Формулација грешке узорковања односи се на формулу која се користи за израчунавање статистичке грешке која се јавља у ситуацији када особа која спроводи тест не одабере узорак који представља целу разматрану популацију и према формули Погрешка узорковања израчунава се дељењем стандардне девијације од популације квадратним кореном величине узорка, а затим множењем резултујуће са вредношћу З која се заснива на интервалу поузданости.

Грешка узорковања = З к (σ /√н)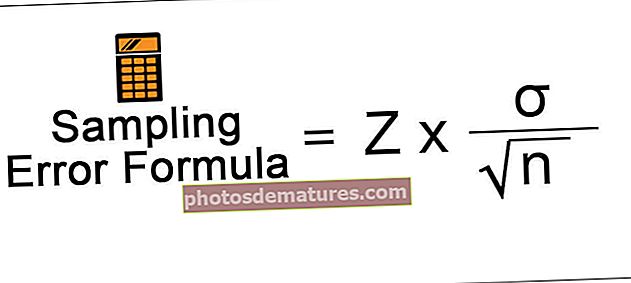

Где,

• З је вредност З резултата на основу интервала поузданости
• σ је стандардна девијација популације
• н је величина узорка

Корак по корак израчунавања грешке узорковања

• Корак 1: Прикупио је све скупове података који се називају становништво. Израчунати средњу вредност популације и стандардну девијацију популације.
• Корак 2: Сада треба одредити величину узорка, а даље величина узорка мора бити мања од популације и не би смела бити већа.
• Корак 3: Одредите ниво поузданости и сходно томе из његове табеле се може утврдити вредност З резултата.
• Корак4: Сада помножите З оцену са стандардном девијацијом популације и поделите је са квадратним кореном величине узорка како бисте дошли до маргине грешке или грешке величине узорка.

Примери

Овде можете преузети овај образац за образац грешке узорака узорака - предложак Екцел образац за грешку узорковања

Пример # 1

Претпоставимо да је стандардна девијација популације 0,30, а величина узорка 100. Колика ће бити грешка узорковања на нивоу поузданости од 95%?

Решење

Овде нам је дата стандардна девијација популације као и величина узорка, стога можемо користити доњу формулу да бисмо израчунали исто.

За израчунавање користите следеће податке.

Стога је израчунавање грешке узорковања следеће,

Грешка у узорковању биће -

Пример # 2

Гаутам тренутно похађа књиговодствени курс и положио је пријемни испит. Сада се регистровао за средњи ниво и такође ће се придружити старијем књиговођи као приправник. Радиће на ревизији производних фирми.

Од једне фирме коју је први пут посетио, затражено је да провери да ли су рачуни за све уносе за куповину разумно доступни. Величина узорка који је изабрао била је 50, а стандардна девијација популације за исти је била 0,50.

На основу доступних информација, потребно је да израчунате грешку узорковања у интервалу поузданости од 95% и 99%.

Решење

Овде нам је дата стандардна девијација популације као и величина узорка, стога можемо користити доњу формулу да бисмо израчунали исто.

З оцена за 95% нивоа поузданости биће 1,96 (доступно из З табеле резултата)

За израчунавање користите следеће податке.

Према томе, прорачун је следећи,

Грешка у узорковању биће -

З оцена за 95% нивоа поузданости биће 2,58 (доступно на З табели резултата)

За израчунавање користите следеће податке.

Према томе, прорачун је следећи,

Грешка у узорковању биће -

Како се ниво поузданости повећава, тако се и грешка узорковања повећава.

Пример # 3

У школи је биометријска сесија организована како би се проверило здравље ученика. Сесија је започета са ученицима одељења Кс стандарда. Укупно има 30 ученика у Б одељењу. Међу њима је 12 ученика насумично одабрано за детаљну проверу, а остало је, урађен је само основни тест. Извештај је закључио да је просечна висина ученика у Б одељењу 154.

Решење

Стандардна девијација становништва износила је 9,39. На основу горе наведених информација, потребно је да израчунате грешку узорковања за интервал поверења од 90% и 95%.

Овде нам је дата стандардна девијација популације као и величина узорка, стога можемо користити доњу формулу за израчунавање истог.

З оцена за 95% нивоа поузданости биће 1,96 (доступно из З табеле резултата)

За израчунавање користите следеће податке.

Стога је израчунавање грешке узорковања следеће,

Грешка у узорковању биће -

З оцена за ниво поузданости од 90% биће 1,645 (доступно из З табеле резултата)

За израчунавање користите следеће податке.

Према томе, прорачун је следећи,

Грешка у узорковању биће -

Како се ниво поузданости смањује, тако се и грешка узорковања смањује.

Релевантност и употреба

За разумевање овог концепта веома је витално, јер ће он приказати колико се може очекивати да би резултати анкете у ствари приказали стварни поглед на укупно становништво. Треба имати на уму да се анкета врши на мањој популацији која се назива величина узорка (која је иначе позната и као испитаници у анкети) како би представљала већу популацију.

Може се посматрати као начин израчунавања ефикасности анкете. Када је маржа узорковања већа, представљаће да би последице истраживања могле да се одступе од стварне укупне заступљености становништва. Са друге стране, грешка у узорковању или маргина грешке је мања од оне која ће указати на то да су последице сада ближе стварној заступљености популације у целини и што ће створити већи ниво поверења у анкету која се прегледава.