photosdematures.com

Дефиниција теорема централне границе

Теорема о централној граници наводи да ће се случајни узорци случајне променљиве популације са било којом расподелом приближити нормалној расподели вероватноће како се величина узорка повећава и претпоставља да ће, како величина узорка у популацији прелази 30, средња вредност узорка чији ће просек свих посматрања за узорак бити б једнак просеку за популацију.

Формула теорема централне границе

Већ смо разговарали о томе да када величина узорка пређе 30, расподела поприма облик нормалне расподеле. За одређивање нормалне расподеле променљиве важно је знати његову средњу вредност и варијансу. Нормална расподела може се навести као

Кс ~ Н (µ, α)

Где

• Н = број запажања
• µ = средња вредност посматрања
• α = стандардна девијација

У већини случајева, запажања не откривају много у сировом облику. Тако да је веома важно стандардизовати запажања како бисмо то могли упоредити. То се ради уз помоћ з-резултата. Потребно је израчунати З-скор за посматрање. Формула за израчунавање з-резултата је

З = (Кс- µ) / α / √н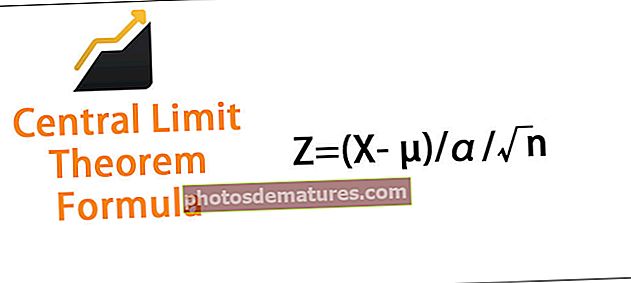

Где

• З = З-оцена запажања
• µ = средња вредност посматрања
• α = стандардна девијација
• н = величина узорка

Објашњење

Теорема о централној граници наводи да ће се случајни узорци случајне променљиве популације са било којом расподелом приближити нормалној расподели вероватноће како се величина узорка повећава. Теорема о централној граници претпоставља да ће, како величина узорка у популацији прелази 30, средња вредност узорка којој ће просек свих посматрања за узорак бити приближно једнак просеку за популацију. Такође, стандардна девијација узорка када величина узорка прелази 30 биће једнака стандардној девијацији популације. Како се узорак насумично бира из целе популације, а величина узорка је већа од 30, онда помаже у тестирању хипотеза и конструисању интервала поузданости за тестирање хипотезе.

Примери формуле теореме централног ограничења (са Екцел предлошком)

Овај предложак формуле формуле теорема централне границе можете преузети овде - образац Екцел формуле теорема централне границе

Пример # 1

Хајде да схватимо концепт нормалне расподеле уз помоћ примера. Просечни принос из узајамног фонда је 12%, а стандардно одступање од средњег поврата за улагање у узајамни фонд је 18%. Ако претпоставимо да се расподела приноса нормално дистрибуира, објаснимо расподелу поврата улагањем узајамног фонда.

Дато,

• Просечни повраћај инвестиције биће 12%
• Стандардна девијација биће 18%

Дакле, да бисмо сазнали поврат за интервал поверења од 95%, то можемо сазнати решавањем једначине као

• Горњи опсег = 12 + 1,96 (18) = 47%
• Доњи опсег = 12 - 1,96 (18) = -23%

Резултат значи да ће 95% пута повраћај из узајамног фонда бити у распону од 47% до -23%. У овом примеру, величина узорка која представља повратак случајног узорка од више од 30 посматрања повратка пружиће нам резултат за повратак становништва узајамног фонда јер ће се дистрибуција узорка нормално дистрибуирати.

Пример # 2

Настављајући са истим примером, одредимо какав ће бити резултат за интервал поузданости од 90%

Дато,

• Просечни повраћај инвестиције биће 12%
• Стандардна девијација биће 18%

Дакле, да бисмо сазнали поврат за интервал поузданости од 90%, то можемо сазнати решавањем једначине као

• Горњи опсег = 12 + 1,65 (18) = 42%
• Доњи опсег = 12 - 1,65 (18) = -18%

Резултат значи да ће у 90% случајева повраћај из узајамног фонда бити у распону од 42% до -18%.

Пример # 3

Настављајући са истим примером, одредимо какав ће бити резултат за интервал поузданости од 99%

Дато,

• Просечни повраћај инвестиције биће 12%
• Стандардна девијација биће 18%

Дакле, да бисмо сазнали поврат за интервал поузданости од 90%, то можемо сазнати решавањем једначине као

• Горњи опсег = 12 + 2,58 (18) = 58%
• Доњи опсег = 12 - 2,58 (18) = -34%

Резултат значи да ће у 99% случајева повраћај из узајамног фонда бити у распону од 58% до -34%.

Релевантност и употреба

Теорема о централној граници је изузетно корисна јер омогућава истраживачу да уз помоћ узорка предвиди средњу вредност и стандардну девијацију целе популације. Како је узорак насумично одабран из целе популације, а величина узорка је већа од 30, тада ће се било која случајна величина узорка узета из популације приближити уобичајеној дистрибуцији, што ће помоћи у тестирању хипотеза и конструисању интервала поузданости за хипотезу тестирање. На основу теореме о централној граници, истраживач је у могућности да изабере било који случајни узорак из целе популације, а када је величина узорка већа од 30, може предвидети популацију уз помоћ узорка јер ће узорак следити нормална расподела и такође као средња вредност и стандардна девијација узорка биће иста као средња вредност и стандардна девијација популације.