photosdematures.com

Хи-квадрат тест са Екцел-ом

Хи-квадрат тест у екцелу је најчешће коришћени непараметарски тест који се користи за поређење две или више променљивих за случајно одабране податке. То је врста теста која се користи за откривање везе између две или више променљивих, ово се користи у статистици која је такође позната и као Хи-квадрат П-вредност, у Екцелу немамо уграђену функцију, али можемо да користимо формуле за извођење хи-квадрат теста у екцелу коришћењем математичке формуле за хи-квадрат тест.

Врсте

1. Хи-квадрат тест за добро прилагођавање
2. Хи-квадрат тест за независност две променљиве.

# 1 - Хи-квадрат тест за добро прилагођавање

Користи се за уочавање близине узорка који одговара становништву. Симбол теста Хи-квадрат је (2). То је збир свих (Запажено бројање - очекивано бројање) 2 / очекивано бројање.

• где је к-1 степен слободе или ДФ.
• Где Ои је посматрана фреквенција, к је категорије, и Еи је очекивана учесталост.

Белешка:- Доброта уклапања статистичког модела односи се на разумевање колико добро подаци узорка одговарају скупу запажања.

Користи

• Кредитна способност зајмопримаца на основу њихових старосних група и личних зајмова
• Веза између перформанси продаваца и стечене обуке
• Поврат на једну деоницу и на акције из сектора попут фармацеутског или банкарског
• Категорија гледалаца и утицај ТВ кампање.

# 2 - Хи-квадрат тест за независност две променљиве

Користи се за проверу да ли су променљиве аутономне једна од друге или не. Са (р-1) (ц-1) степеном слободе

Где Ои је посматрана фреквенција, р је број редова, ц је број колона и Еи је очекивана учесталост

Белешка:- Две случајне променљиве називају се неовисним ако друга не утиче на расподелу вероватноће једне променљиве.

Користи

Тест независности погодан је за следеће ситуације:

• Постоји једна категоричка променљива.
• Постоје две категоричке променљиве и мораћете да утврдите везу између њих.
• Постоје унакрсне табеле и треба пронаћи везу између две категоричке променљиве.
• Постоје променљиве које се не могу мерити (на пример, одговори на питања попут тога, да ли запослени у различитим старосним групама бирају различите врсте здравствених планова?)

Како урадити тест хи-квадрат у програму Екцел? (са примером)

Овде можете преузети овај предложак за тестирање Цхи Скуаре-а - Екцел предложак за тестирање квадрата

Менаџер ресторана жели да пронађе везу између задовољства купаца и плата људи који чекају столове. У овоме ћемо поставити хипотезу за тестирање хи-квадрата

• Узима насумични узорак од 100 купаца који питају да ли је услуга била одлична, добра или лоша.
• Потом она категорише плате људи који чекају као ниске, средње и високе.
• Претпоставимо да је ниво значајности 0,05. Овде Х0 и Х1 означавају независност и зависност квалитета услуге од плата људи који чекају.
• Х.₀ - квалитет услуге не зависи од плата људи који чекају столове.
• Х.₁ - квалитет услуге зависи од плата људи који чекају столове
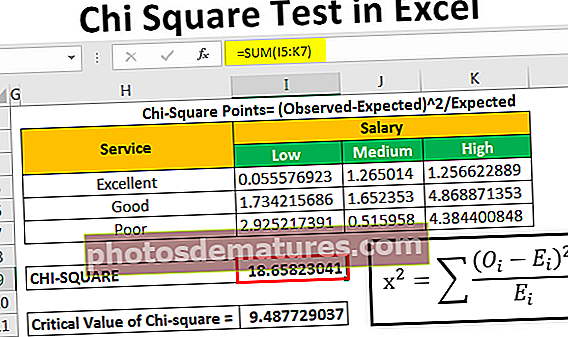
• Њени налази су приказани у доњој табели:

У овом случају имамо 9 тачака података, имамо 3 групе од којих је свака добила другачију поруку о плати, а исход је дат у наставку.

Сада ћемо пребројати збир свих редова и колона. То ћемо учинити уз помоћ формуле тј. СУМ. Укупан резултат Одлично у укупној колони коју смо написали = СУМ (Б4: Д4) а затим притисните ентер.

Ово ће нам дати 26. Исто ћемо извршити са свим редовима и колонама.

Да бисте израчунали Степен слободе (ДФ) користимо (р-1) (ц-1)

ДФ = (3-1)(3-1)=2*2=4

• Постоје 3 категорије услуга и 3 категорије плата
• Имамо 27 испитаника са средњом платом (доњи ред, средина)
• Имамо 51 испитаника са добром услугом (последња колона, средња)

Сада морамо израчунати Очекиване фреквенције: -

Очекиване фреквенције може се израчунати помоћу формуле: -

• Да бисте израчунали за Одлицно користићемо множењем укупног броја Ниска са укупно Одлично подељено од Н.

Претпоставимо да морамо израчунати за 1. ред и 1. колону (= Б7 * Е4 / Б9). То ће дати очекивани број купаца који су гласали Одлицно служба за плате људи који чекају као ниска односно 8.32.

• Е.₁₁₌­­(32*26)/100 = 8.32, Е.₁₂ = 7.02, Е.₁₃ = 10.66
• Е.₂₁ = 16.32, Е.₂₂ = 13.77, Е.₂₃ = 20.91
• Е.₃₁ = 7.36, Е.₃₂ = 6.21, Е.₃₃ = 9.41

Слично за све, и ми морамо да урадимо исто, а формула је примењена на доњем дијаграму.

Добијамо табелу очекиване фреквенције како је дато у наставку: -

Белешка:- Претпоставимо да је ниво значајности 0,05. Овде Х0 и Х1 означавају независност и зависност квалитета услуге од плата људи који чекају.

Након израчунавања очекиване фреквенције израчунаћемо тачке података хи-квадрат користећи формулу

Хи-квадрат поени = (Посматрано-Очекивано) ^ 2 / Очекивано

Да бисмо израчунали прву тачку коју пишемо = (Б4-Б14) ^ 2 / Б14.

Формулу ћемо копирати и залепити у друге ћелије да бисмо аутоматски попунили вредност.

После овога израчунаћемо цхи-валуе (израчуната вредност) додавањем свих вредности датих изнад табеле

Добили смо Цхи-вредност као 18.65823.

За израчунавање критичне вредности за ово користимо хи-квадрат табелу критичних вредности, а можемо користити формулу која је дата у наставку.

Ова формула садржи 2 параметра ЦХИСК.ИНВ.РТ (вероватноћа, степен слободе).

Вероватноћа је 0,05, то је значајна вредност која ће нам помоћи да одредимо да ли да прихватимо Нулта хипотеза (Х.₀) или не.

Критична вредност хи-квадрата је 9.487729037.

Сада ћемо пронаћи вредност хи-квадрат или (вредност П)= ЦХИТЕСТ (стварни_домет, очекивани_опсег)

Распон од = ЦХИТЕСТ (Б4: Д6, Б14: Д16).

Као што смо видели да је вредност цхи-теста или П-вредности = 0,00091723.

Као што смо видели да смо израчунали све вредности. Тхе хи-квадрат (израчуната вредност) вредности су значајне само када је његова вредност иста или већа од вредности критична вредност 9,48, тј. критична вредност (табеларна вредност) мора бити већи од 18.65 да прихвате Нулта хипотеза (Х.₀).

Али овде Израчуната вредност >Табеларна вредност

Кс2 (израчунато)> Кс2 (табеларно)

18.65>9.48

У овом случају ћемо одбити Нулта хипотеза (Х.₀) и Алтернативни (Х.₁) биће прихваћен.

• Такође можемо користити П-вредност да бисмо предвидели исто, тј П-вредност <= α (значајна вредност 0,05), Нулта хипотеза ће бити одбачена
• Ако је П-вредност> α, немој одбаци нулта хипотеза.

Ево П-вредност (0,0009172)< α (0,05), одбити Х.₀, прихвати Х.₁

Из горњег примера закључујемо да квалитет услуге зависи од плата људи који чекају.

Ствари које треба запамтити

• Разматра квадрат стандардне нормалне варијабле.
• Процењује да ли се фреквенције уочене у различитим категоријама значајно разликују од фреквенција које се очекују под одређеним скупом претпоставки.
• Одређује колико претпостављена дистрибуција одговара подацима.
• Користи табеле за непредвиђене случајеве (у истраживањима тржишта ове табеле се називају унакрсни табови).
• Подржава мерења на номиналном нивоу.