photosdematures.com

Шта је прилагођени Р квадрат?

Прилагођени Р Скуаред односи се на статистички алат који помаже инвеститорима у мерењу обима варијансе варијабле која је зависна и која се може објаснити независном променљивом, а узима у обзир утицај само оних независних варијабли које имају утицај на варијацију зависне променљиве.

Прилагођени Р квадрат или модификовани Р ^ 2 одређује опсег варијансе зависне променљиве која се може објаснити независном променљивом. Посебност модификованог Р ^ 2 је што не узима у обзир утицај свих независних променљивих, већ само оних које утичу на варијацију зависне променљиве. Вредност модификованог Р ^ 2 такође може бити негативна, мада већину времена није негативна.

Прилагођена Р формула у квадрату

Формула за израчунавање прилагођеног Р кваса регресије представљена је као испод,

Р ^ 2 = {(1 / Н) * Σ [(ки - к) * (ии - и)] / (σк * σи)} ^ 2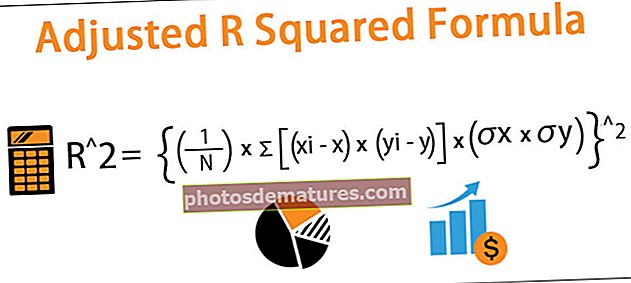

Где

• Р ^ 2 = прилагођени Р квадрат регресионе једначине
• Н = Број запажања у регресионој једначини
• Кси = Независна променљива регресионе једначине
• Кс = Средња вредност независне променљиве регресионе једначине
• Ии = Зависна променљива регресионе једначине
• И = Средња вредност зависне променљиве регресионе једначине
• σк = Стандардна девијација независне променљиве
• σи = Стандардна девијација зависне променљиве.

Молим обратите пажњу

За израчунавање у екцелу потребно је обезбедити и и к променљиве у екцелу, а цео излаз заједно са прилагођеним Р ^ 2 генерише Екцел. Посебан је случај када је тешко пружити излаз у текстуалном формату, за разлику од других формула.

Тумачење

Прилагођени Р квадрат одређује опсег варијансе зависне променљиве која се може објаснити независном променљивом. Гледајући прилагођену вредност Р ^ 2 може се судити да ли се подаци у регресионој једначини добро уклапају. Што је већа прилагођена Р ^ 2, боље је регресиона једначина, јер подразумева да је независна променљива изабрана да би се одредила зависна променљива у стању да објасни варијацију у зависној променљивој.

Вредност модификованог Р ^ 2 такође може бити негативна, мада већину времена није негативна. У случају прилагођеног Р квадрата, вредност прилагођеног Р квадрата ће расти са додавањем независне променљиве само када варијација независне променљиве утиче на варијацију зависне променљиве. Ово није применљиво у случају Р ^ 2, применљиво само на вредност прилагођеног Р ^ 2.

Примери

Овде можете да преузмете овај Прилагођени Р Скуаред Формула Екцел образац - Прилагођени Р Скуаред Формула Екцел Предложак

Пример # 1

Покушајмо да схватимо концепт прилагођеног Р ^ 2 помоћу примера. Покушајмо да откријемо какав је однос између удаљености коју је прешао возач камиона и старости возача камиона. Неко заправо врши регресиону једначину да би потврдио да ли оно што мисли о односу две променљиве валидира и регресиона једначина.

У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој једначини регресије је удаљеност коју пређе возач камиона, а независна променљива је старост возача камиона. Покретањем регресије са променљивим добили смо прилагођени Р квадрат од 65%. Снимак испод приказује регресиони излаз за променљиве. Скуп података и променљиве представљени су у приложеном екцел листу.

Прилагођена вредност Р ^ 2 од 65% за ову регресију подразумева да се 65% варијације у зависној променљивој објашњава независном променљивом. У идеалном случају, истраживач ће тражити коефицијент утврђености који је најближи 100%.

Пример # 2

Покушајмо да схватимо концепт прилагођеног Р квадрата уз помоћ другог примера. Покушајмо да откријемо какав је однос између висине ученика одељења и просечне оцене тих ученика. У овом конкретном примеру видећемо која је променљива зависна, а која независна променљива. Зависна променљива у овој једначини регресије је просек успеха ученика, а независна променљива висина ученика.

Покретањем регресије са променљивим добили смо прилагођени Р ^ 2 да буде занемарљив или негативан. Снимак испод приказује регресиони излаз за променљиве. Скуп података и променљиве представљени су у приложеном екцел листу.

Прилагођена вредност Р ^ 2 је занемарљива за ову регресију, што подразумева да варијација у зависној променљивој није објашњена независном променљивом. У идеалном случају, истраживач ће тражити коефицијент утврђености који је најближи 100%.

Тумачење

Прилагођени квадрат Р веома је важан излаз како би се сазнало да ли је скуп података добро уклапан или не. Неко у ствари врши регресиону једначину да би потврдио да ли оно што мисли о односу две променљиве валидира и регресиона једначина. Што је већа вредност, то је једначина регресије боља јер подразумева да је независна променљива изабрана да би се одредила зависна променљива правилно изабрана. У идеалном случају, истраживач ће тражити коефицијент утврђености који је најближи 100%.