photosdematures.com

СИН Екцел функција је уграђена тригонометријска функција у екцелу која се користи за израчунавање синусне вредности датог броја или у смислу тригонометрије синусне вредности датог угла, овде је угао број у екцелу и ова функција узима само један аргумент што је наведени улазни број.

СИН функција у програму Екцел

СИН функција у програму Екцел израчунава синус угла који одредимо. Функција СИН у програму Екцел категорисана је као функција математике / тригонометрије у програму Екцел. СИН у Екцелу увек враћа нумеричку вредност.

У математици и тригонометрији СИНЕ је тригонометријска функција угла, који је у правоуглом троуглу једнак дужини супротне странице (правоугаоне странице), подељен дужином хипотенузе и представљен као :

Син Θ = супротна страна / хипотенуза

Син Θ = а / х

СИН формула у Екцелу

Испод је СИН формула у програму Екцел.

Где је број аргумент прослеђен СИН формули у радијанима.

Ако директно пренесемо угао на СИН у екцел функцији, он га неће препознати као ваљан аргумент. На пример, ако проследимо 30 ° као аргумент овом СИН-у у Екцел функцији, неће га препознати као важећи аргумент. Екцел ће приказати поруку о грешци.

Дакле, аргумент који треба да пренесемо мора бити у радијани.

Постоје две методе за претварање угла у радијан

1. Користите уграђену Екцел РАДИАНС функцију. Функција РАДИАНС претвара степене у вредност радијана.

На пример, за претварање 30 ° у радијан користићемо ову функцију, узима се степен као број, а 30 ° као 30.

=РАДИЈАНИ (30) даће радијан 0,52

2. У другом случају можемо користити математичку формулу за претварање степена у радијан. Формула је

Радиан = степени * (π / 180) (π = 3,14)

У Екцелу такође имају функцију која враћа вредност Пи, тачну на 15 цифара, а функција је ПИ ()

Стога бисмо за конверзију степена у радијан користили формулу

Радиан = степени * (ПИ () / 180)

Како се користи СИН функција у програму Екцел?

СИН функција у програму Екцел је врло једноставна и лака за употребу. Нека неки примери примере рад СИН-а у екцелу.

Овај СИН у Екцел предлошку можете преузети овде - СИН у Екцел предлошку

СИН у Екцелу Пример # 1

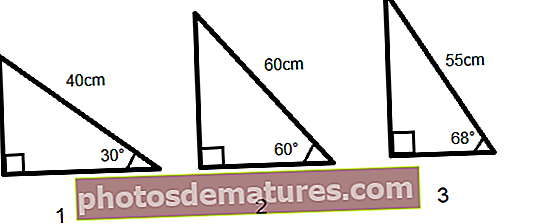
Израчунавање вредности синуса помоћу функције СИН у програму Екцел и функције РАДИАНС у програму Екцел

Израчунавање вредности синуса помоћу функције СИН у програму Екцел и функције ПИ

Функција синуса у програму Екцел има много апликација у стварном животу; широко се користи у архитектури за израчунавање висина и дужина геометријских фигура. Такође се користи у ГПС-у, оптици, израчунавању путања, за проналажење најкраће руте на основу географске ширине и дужине, географског положаја, радио емитовања итд. Чак је и електромагнетни талас уцртан као графикон функције синуса и косинуса.

Претпоставимо да имамо три правоугаона троугла дата са њиховим угловима и дужином једне странице и да морамо израчунати дужину друге две странице.

Збир свих углова на троуглу једнак је 180 °, стога трећи угао можемо лако израчунати.

Знамо, Син Θ = супротност / хипотенуза

Дакле, дужина супротне стране ће бити Син Θ * хипотенуза

У Екцелу ће се дужина супротне странице (окомите странице) израчунати према СИН формули

= ГРЕХ (РАДИЈАНИ (Ц2)) * Е2

Применом горе дате СИН формуле за три троугла можемо добити дужину окомитих троуглова

За трећу страну (суседну страну) имамо две методе - коришћењем Питагорине теореме или поновним коришћењем функције СИН у програму Екцел из других углова.

Према Питагориној теореми, збир квадрата две странице правоуглог троугла еквивалентан је квадрату хипотенузе.

Хипотенуза2 = Насупрот2 + Суседна2

Суседни = (Хипотенуза2 - Насупрот2) 1/2

У Екцелу ћемо то написати као,

= СНАГА ((МОЋ (Хипотенуза, 2) -МОЋ (Супротно, 2)), 1/2)

Примењујући ову формулу, израчунавамо дужину суседне странице

= СНАГА ((СНАГА (Е2,2)-СНАГА (Ф2,2)), 1/2)

Користећи другу методу, можемо да користимо СИНЕ 3. угла за израчунавање вредности суседне странице

Ако ротирамо троуглове за 90 ° улево, супротна страница се замењује суседном страном, а СИН угла између хипотенузе и суседне помоћи ће да се израчуна вредност треће странице.

= ГРЕХ (РАДИЈАНИ (Д2)) * Е2

СИН у Екцелу Пример # 2

Постоји висока зграда непознате висине и Сунчев зрак у тренутку прави угао у тачки А од 75 °, чинећи тако сенку зграде дужине 70 метара. Морамо пронаћи висину куле

Висина зграде израчунава се помоћу СИН у екцел функцији

СИН 75 ° = Висина грађевине / дужина сенке у тачки А

Према томе, висина зграде = СИН 75 ° * Дужина сенке у тачки А

Отуда ће бити висина градње

= ГРЕХ (РАДИЈАНИ (Б3)) * Б2

Висина зграде је 67,61 метара

СИН у Екцелу Пример # 3

Имамо копно у облику троугла, за који су два угла дата као 30 ° и 70 °, а знамо само дужину једне странице троугла која је 40 метара. Морамо пронаћи дужину остале три странице и обод троугла.

За троугао, када су позната једна страница и сви углови, можемо израчунати остале странице по СИНЕ правилу

Правило синуса у тригонометрији даје однос углова греха и страница троугла према СИН формули

а / син α = б / син ß = ц / син δ

У овом случају,

α = 30 °, ß = 70 ° и δ = 180 ° - (30 ° + 70 °) = 80 ° и једна страница троугла б = 40 метара

Да бисмо пронашли остале странице троугла, користићемо правило СИНЕ

а = Син α * (б / син ß)

Стога,

а = ГРЕХ (РАДИЈАНИ (30)) * (Б5 / СИН (РАДИЈАНИ (70)))

Дужина странице а = 21,28 метара

Слично томе, биће и трећа страна ц

ц = Син δ * (б / син ß)

Стога,

ц = ГРЕХ (РАДИЈАНИ (80)) * (Б5 / СИН (РАДИЈАНИ (70)))

Три странице троугла су дужине 21,28, 40, 41,92 метра.

Опсег троугла је збир свих страница.

Стога ће периметар бити = СУМ (Б5: Б7)